Lösung von Aufg. 12.1 S: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
Zeile 2: Zeile 2:
 
Man beweise: Ein Punkt <math>\ P</math> gehört genau dann zur Winkelhalbierenden des Winkels <math>\ \alpha</math>, wenn er zu den Schenkeln von <math>\ \alpha</math> jeweils denselben Abstand hat.<br />
 
Man beweise: Ein Punkt <math>\ P</math> gehört genau dann zur Winkelhalbierenden des Winkels <math>\ \alpha</math>, wenn er zu den Schenkeln von <math>\ \alpha</math> jeweils denselben Abstand hat.<br />
  
−
Lösungsversuch Lerngruppe Nummero6/Tchu Tcha Tcha:<br />
+
'''Lösungsversuch Lerngruppe Nummero6/Tchu Tcha Tcha:'''<br />
  
 
d.h.<br />
 
d.h.<br />
 
'''1)'''<math>P\in w_\alpha \Rightarrow \left| \ P,SA^{+} \right| \tilde {=} \left| \ P,SB^{+} \right|</math><br />
 
'''1)'''<math>P\in w_\alpha \Rightarrow \left| \ P,SA^{+} \right| \tilde {=} \left| \ P,SB^{+} \right|</math><br />
 
'''2)'''<math>\left| \ P,SA^{+} \right| \tilde {=} \left| \ P,SB^{+} \right| \Rightarrow P\in w_\alpha</math><br />
 
'''2)'''<math>\left| \ P,SA^{+} \right| \tilde {=} \left| \ P,SB^{+} \right| \Rightarrow P\in w_\alpha</math><br />
−
Skizze folgt..
 
 
<br />
 
<br />
−
'''zu 1)'''<br />
+
<br />
 +
'''zu 1)'''[[Datei:Übung 12.1 Beweis1.png]]
 +
<br />
 
(1)<math>\left| \angle BSP  \right| = \left| \gamma  \right| \tilde {=} \left| \angle PSA  \right| = \left| \beta  \right|</math> // Vor.<br />
 
(1)<math>\left| \angle BSP  \right| = \left| \gamma  \right| \tilde {=} \left| \angle PSA  \right| = \left| \beta  \right|</math> // Vor.<br />
 
(2)<math>\overline{SP} \tilde {=} \overline{SP}</math> // trivial<br />
 
(2)<math>\overline{SP} \tilde {=} \overline{SP}</math> // trivial<br />
Zeile 20: Zeile 21:
 
(9)<math>\overline{P L_A} \tilde {=} \overline{P L_B}</math> // (7), Dreieckskongruenz<br />
 
(9)<math>\overline{P L_A} \tilde {=} \overline{P L_B}</math> // (7), Dreieckskongruenz<br />
 
qed<br />
 
qed<br />
−
'''zu 2)'''<br />
+
'''zu 2)'''[[Datei:Übung 12.1 Beweis2.png]]
 +
<br />
 
(1) <math>\overline{SP}  \tilde {=} \overline{SP}</math> // trivial<br />
 
(1) <math>\overline{SP}  \tilde {=} \overline{SP}</math> // trivial<br />
 
(2)<math>\left| \ P,SA^{+} \right| \tilde {=} \left| \ P,SB^{+} \right|</math> // Voraussetzung<br />
 
(2)<math>\left| \ P,SA^{+} \right| \tilde {=} \left| \ P,SB^{+} \right|</math> // Voraussetzung<br />

Aktuelle Version vom 13. Juli 2012, 14:35 Uhr

Aufgabe 12.1

Man beweise: Ein Punkt \ P gehört genau dann zur Winkelhalbierenden des Winkels \ \alpha, wenn er zu den Schenkeln von \ \alpha jeweils denselben Abstand hat.

Lösungsversuch Lerngruppe Nummero6/Tchu Tcha Tcha:

d.h.
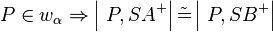
1)P\in w_\alpha \Rightarrow \left| \ P,SA^{+} \right| \tilde {=} \left| \ P,SB^{+} \right|
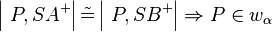
2)\left| \ P,SA^{+} \right| \tilde {=} \left| \ P,SB^{+} \right| \Rightarrow P\in w_\alpha


zu 1)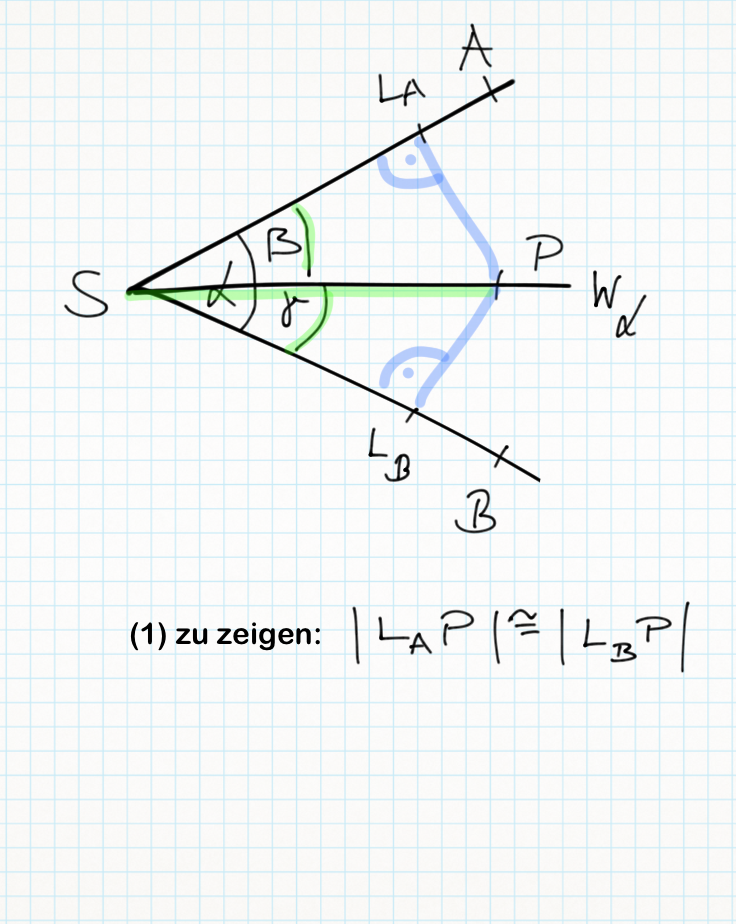Übung 12.1 Beweis1.png
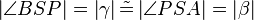(1)\left| \angle BSP \right| = \left| \gamma \right| \tilde {=} \left| \angle PSA \right| = \left| \beta \right| // Vor.
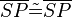(2)\overline{SP} \tilde {=} \overline{SP} // trivial
(3)Fehler beim Parsen(Syntaxfehler): \exists l_1:l_1 \cap w_\alpha=\{P}\wedge l_1 \cap SA=\{L_A}\wedge l_1 \perp SA 

// Ex. & Eind. der Senkrechten durch P zu SA

(4) 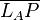\overline{L_A P} ist Lot // (3), Def. Lot
(5)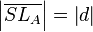\left| \overline{S L_A} \right| = \left| d \right| // Axiom II/1 (Abstandsaxiom)
(6)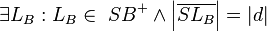\exists L_B:L_B \in \ SB^{+} \wedge \left| \overline{S L_B} \right| = \left| d \right| // Axiom v. Lineal, (5)
(7)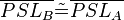\overline{PS L_B} \tilde {=} \overline{PS L_A} // (1),(2),(5),(6), SWS
(8)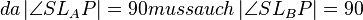da \left| \angle SL_AP \right| = 90 muss auch \left| \angle SL_BP \right| = 90 // (3),(7), Dreieckskongruenz
(9)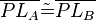\overline{P L_A} \tilde {=} \overline{P L_B} // (7), Dreieckskongruenz
qed
zu 2)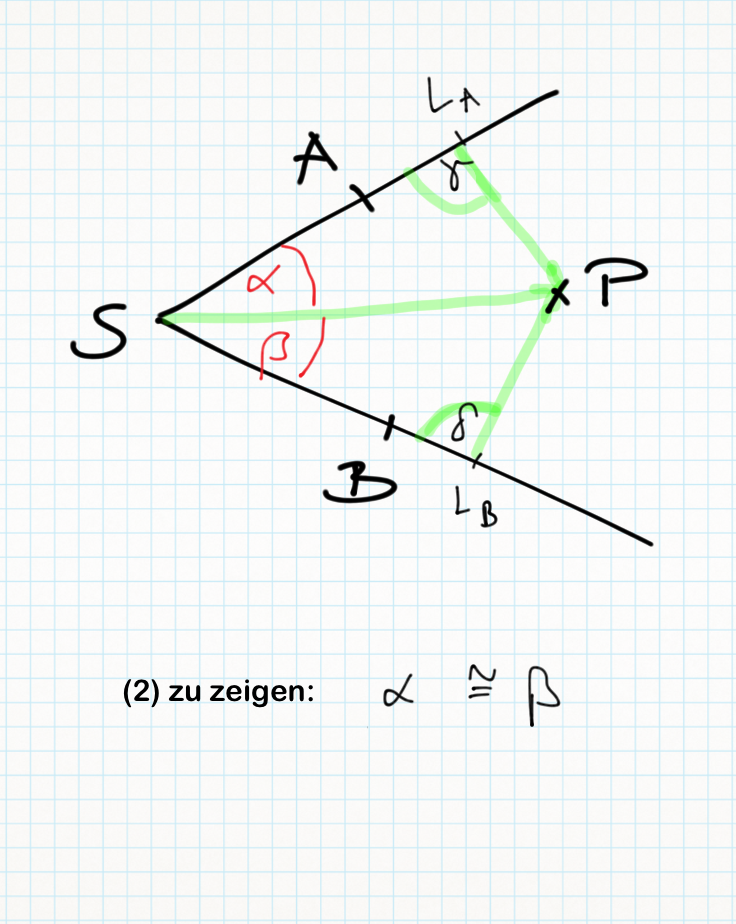Übung 12.1 Beweis2.png
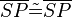(1) \overline{SP} \tilde {=} \overline{SP} // trivial
(2)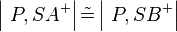\left| \ P,SA^{+} \right| \tilde {=} \left| \ P,SB^{+} \right| // Voraussetzung
(3)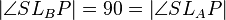\left| \angle SL_BP \right| = 90 = \left| \angle SL_AP \right| // Def. Lotgerade
(4) 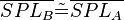\overline{SPL_B} \tilde {=} \overline{SPL_A} // (1-3), SsW
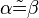(5) \alpha \tilde {=} \beta // (4), Dreieckskongruenz
qed
--Tchu Tcha Tcha 14:23, 13. Jul. 2012 (CEST)


Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._12.1_S&oldid=16626“