Lösung von Aufg. 12.3 S: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Beweisen Sie: Wenn <math>\ P</math> ein Punkt außerhalb der Geraden <math>\ g</math> ist, dann gibt es eine Gerade <math>\ h</math>, die durch <math>\ P</math> g…“) |
|||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Wenn <math>\ P</math> ein Punkt außerhalb der Geraden <math>\ g</math> ist, dann gibt es eine Gerade <math>\ h</math>, die durch <math>\ P</math> geht und parellel zu <math>\ g</math> ist. | Beweisen Sie: Wenn <math>\ P</math> ein Punkt außerhalb der Geraden <math>\ g</math> ist, dann gibt es eine Gerade <math>\ h</math>, die durch <math>\ P</math> geht und parellel zu <math>\ g</math> ist. | ||
| + | <br /> | ||
| + | |||
| + | '''Lösungsversuch Nummero6/Tchu Tcha Tcha:'''<br /> | ||
| + | Vor.: Gerade g, Punkt <math>P \not\in g</math><br /> | ||
| + | Beh.: Es gibt eine Gerade <math>h</math>, die durch <math>P</math> geht und parellel zu <math>g</math> ist.<br /> | ||
| + | Annahme: Es gibt KEINE Gerade <math>h</math>, die durch <math>P</math> geht und parellel zu <math>g</math> ist.<br /> | ||
| + | [[Datei:Übung 12.3.png]] | ||
| + | <br /> | ||
| + | |||
| + | (1) <math>\exists i</math>: <math>P \in i \wedge i \not \equiv g \wedge \ i \cap g = \{S} </math> mit dem Schnittpunkt <math>S</math><br /> | ||
| + | (2) <math>\left|\angle ASP \right| = \left| w \right|</math> // (1),Winkelmaßaxiom (ab sofort gilt zur Vereinfachung, vgl. Skizze,<math>\alpha = \angle ASP</math>) <br /> | ||
| + | (3) Es gibt einen Winkel <math>\alpha '</math> in der Halbebene <math>\ SP,A^{+}</math> für den gilt: <math>\left| w \right| = \left|\angle\alpha' \right|</math> // Winkelkonstruktionsaxiom (2), Voraussetzung<br /> | ||
| + | (4) <math>\alpha \tilde {=} \alpha'</math> // (1-3), Def. Stufenwinkel<br /> | ||
| + | (5) <math>g\|| h</math> // (4), Umkehrung des Stufenwinkelsatzes<br /> | ||
| + | (6) Widerspruch zur Annahme // (5)<br /> | ||
| + | (7) Behauptung stimmt // (6)<br /> | ||
| + | qed<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 16:28, 13. Jul. 2012 (CEST) | ||
<br /> | <br /> | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 13. Juli 2012, 15:28 Uhr
Beweisen Sie: Wenn  ein Punkt außerhalb der Geraden
ein Punkt außerhalb der Geraden  ist, dann gibt es eine Gerade
ist, dann gibt es eine Gerade  , die durch
, die durch  geht und parellel zu
geht und parellel zu  ist.
ist.
Lösungsversuch Nummero6/Tchu Tcha Tcha:
Vor.: Gerade g, Punkt 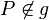
Beh.: Es gibt eine Gerade  , die durch
, die durch  geht und parellel zu
geht und parellel zu  ist.
ist.
Annahme: Es gibt KEINE Gerade  , die durch
, die durch  geht und parellel zu
geht und parellel zu  ist.
ist.
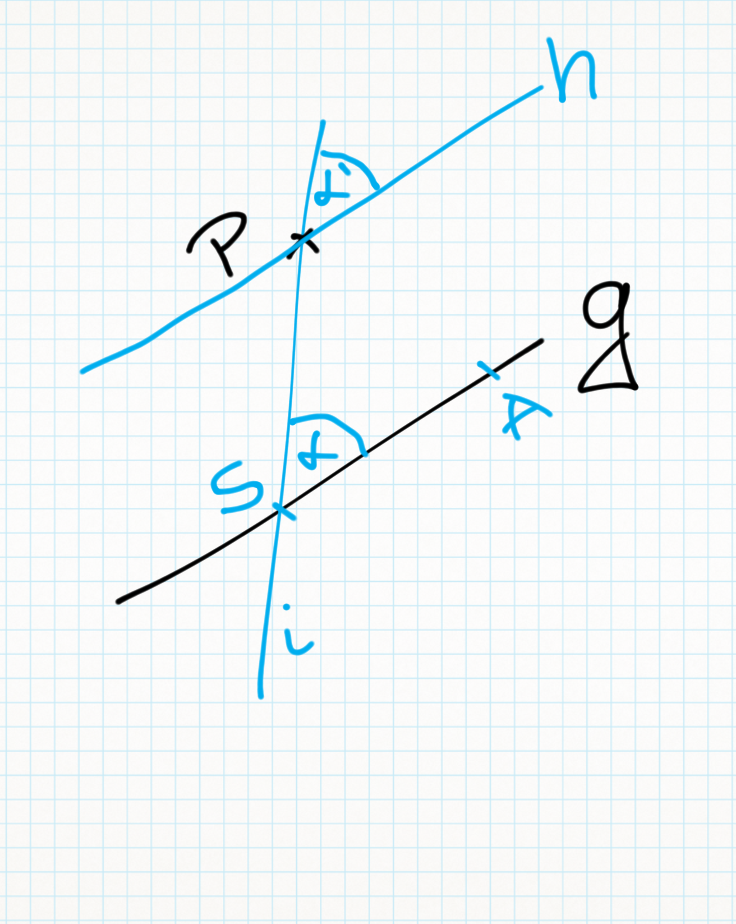
(1) 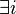 : Fehler beim Parsen(Syntaxfehler): P \in i \wedge i \not \equiv g \wedge \ i \cap g = \{S}
: Fehler beim Parsen(Syntaxfehler): P \in i \wedge i \not \equiv g \wedge \ i \cap g = \{S}
mit dem Schnittpunkt
(2) 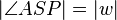 // (1),Winkelmaßaxiom (ab sofort gilt zur Vereinfachung, vgl. Skizze,
// (1),Winkelmaßaxiom (ab sofort gilt zur Vereinfachung, vgl. Skizze,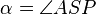 )
)
(3) Es gibt einen Winkel 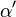 in der Halbebene
in der Halbebene 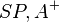 für den gilt:
für den gilt: 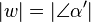 // Winkelkonstruktionsaxiom (2), Voraussetzung
// Winkelkonstruktionsaxiom (2), Voraussetzung
(4) 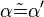 // (1-3), Def. Stufenwinkel
// (1-3), Def. Stufenwinkel
(5) 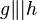 // (4), Umkehrung des Stufenwinkelsatzes
// (4), Umkehrung des Stufenwinkelsatzes
(6) Widerspruch zur Annahme // (5)
(7) Behauptung stimmt // (6)
qed
--Tchu Tcha Tcha 16:28, 13. Jul. 2012 (CEST)


