Lösung von Testaufgabe 2.1 SS12: Unterschied zwischen den Versionen
Mahe84 (Diskussion | Beiträge) |
|||
| Zeile 9: | Zeile 9: | ||
Es seien A,B,C,D vier kollineare Punkte, von denen zwei jeweils paarweise kollinear sind. | Es seien A,B,C,D vier kollineare Punkte, von denen zwei jeweils paarweise kollinear sind. | ||
Eine Figur mit der Vereinigungsmenge aus <math>\overline{AB} </math>, <math>\overline{BC} </math>, <math>\overline{CD} </math>, <math>\overline{DA} </math>, ist ein Viereck.--[[Benutzer:Mahe84|Mahe84]] 17:04, 14. Jul. 2012 (CEST) | Eine Figur mit der Vereinigungsmenge aus <math>\overline{AB} </math>, <math>\overline{BC} </math>, <math>\overline{CD} </math>, <math>\overline{DA} </math>, ist ein Viereck.--[[Benutzer:Mahe84|Mahe84]] 17:04, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | Es seien A, B, C und D vier paarweise verschiedene Pnkte ein und derselben Ebene. JE drei der Punkte seien nich kollinear. Die Vereinigungsmenge der Strecken <math>\overline{AB} </math>, <math>\overline{BC} </math>, <math>\overline{CD} </math> und <math>\overline{DA} </math> heißt Viereck.--[[Benutzer:*osterhase*|*osterhase*]] 17:23, 14. Jul. 2012 (CEST) | ||
Version vom 14. Juli 2012, 16:23 Uhr
Es seien A,B,C,D vier Punkte die alle in einer Ebene liegen und nicht kollinear sind.
Unter dem Viereck ABCD versteht man die Punktmenge:  vereinigt mit
vereinigt mit  vereinigt mit
vereinigt mit 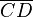 vereinigt mit
vereinigt mit 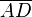 --Funkdocta 11:33, 14. Jul. 2012 (CEST)
--Funkdocta 11:33, 14. Jul. 2012 (CEST)
Es seien A,B,C,D vier Punkte. Die Punkte A,B,C,D seien komplanar und jeweils zwei von ihnen kollinear. Die Vereinigungsmenge der Strecken AB,BC,CD,AD bilden das Viereck ABCD.--Celebino 11:44, 14. Jul. 2012 (CEST)
Ist beides nicht ganz korrekt.--*m.g.* 14:20, 14. Jul. 2012 (CEST)
Es seien A,B,C,D vier kollineare Punkte, von denen zwei jeweils paarweise kollinear sind.
Eine Figur mit der Vereinigungsmenge aus  ,
,  ,
, 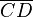 ,
, 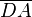 , ist ein Viereck.--Mahe84 17:04, 14. Jul. 2012 (CEST)
, ist ein Viereck.--Mahe84 17:04, 14. Jul. 2012 (CEST)
Es seien A, B, C und D vier paarweise verschiedene Pnkte ein und derselben Ebene. JE drei der Punkte seien nich kollinear. Die Vereinigungsmenge der Strecken  ,
,  ,
, 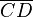 und
und 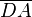 heißt Viereck.--*osterhase* 17:23, 14. Jul. 2012 (CEST)
heißt Viereck.--*osterhase* 17:23, 14. Jul. 2012 (CEST)

