Lösung von Testaufgabe 2.5 SS12: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 10: | Zeile 10: | ||
Wenn der Winkel ABC ein rechter ist, dann liegt der Punkt C nicht im Inneren von k. --[[Benutzer:LuLu7410|LuLu7410]] 19:18, 14. Jul. 2012 (CEST) | Wenn der Winkel ABC ein rechter ist, dann liegt der Punkt C nicht im Inneren von k. --[[Benutzer:LuLu7410|LuLu7410]] 19:18, 14. Jul. 2012 (CEST) | ||
| + | <br /> | ||
| + | Wenn der Winkel <math>\gamma = \angle ACB</math> ein rechter Winkel ist, dann liegt der Punkt <math>C</math> nicht im Inneren von k.--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 19:21, 14. Jul. 2012 (CEST) | ||
Version vom 14. Juli 2012, 18:21 Uhr
Kontraposition:
Der Winkel ist ein rechter Winkel, wenn der Punkt C auf dem Kreis k liegt. --Funkdocta 12:41, 14. Jul. 2012 (CEST)
Vorsicht: Nicht vom Thalessatz verführen lassen. Sie haben zwar eine wahre Aussage formuliert, jedoch nicht die exakte Kontraposition der Implikation, die vorgegeben war.--*m.g.* 14:19, 14. Jul. 2012 (CEST)
Kontraposition:
Ist der Winkel 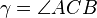 ein rechter Winkel, liegt der Punkt C nicht im Inneren von k.--Mahe84 17:49, 14. Jul. 2012 (CEST)
ein rechter Winkel, liegt der Punkt C nicht im Inneren von k.--Mahe84 17:49, 14. Jul. 2012 (CEST)
Wenn der Winkel ABC ein rechter ist, dann liegt der Punkt C nicht im Inneren von k. --LuLu7410 19:18, 14. Jul. 2012 (CEST)
Wenn der Winkel 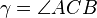 ein rechter Winkel ist, dann liegt der Punkt
ein rechter Winkel ist, dann liegt der Punkt  nicht im Inneren von k.--Tchu Tcha Tcha 19:21, 14. Jul. 2012 (CEST)
nicht im Inneren von k.--Tchu Tcha Tcha 19:21, 14. Jul. 2012 (CEST)

