Lösungsidee Übung Heckl Aufgabe 11.6 SoSe2012: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
HecklF (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „== Aufgabe 11.6 == Beweisen Sie: Sei <math>P</math> ein Punkt und <math>g</math> eine Gerade. Es existiert genau ein Lot von <math>P</math> auf <math>g</math>. <…“) |
HecklF (Diskussion | Beiträge) (→Aufgabe 11.6) |
||
| Zeile 11: | Zeile 11: | ||
|} | |} | ||
<br /> | <br /> | ||
| − | Wir | + | Wir KÖNNTEN folgende Fälle unterscheiden: |
* Punkt A liegt derart, dass <math>PA \ \perp \ g</math> gilt, dann wären wir fertig | * Punkt A liegt derart, dass <math>PA \ \perp \ g</math> gilt, dann wären wir fertig | ||
* wir könnten auch den Fall annehmen, dass <math>\angle PAB</math> so liegt, dass es der Außenwinkel von <math>\alpha</math> ist - dann müssten wir dies in unsere Beweisführung einplanen. | * wir könnten auch den Fall annehmen, dass <math>\angle PAB</math> so liegt, dass es der Außenwinkel von <math>\alpha</math> ist - dann müssten wir dies in unsere Beweisführung einplanen. | ||
Version vom 15. Juli 2012, 13:48 Uhr
Aufgabe 11.6
Beweisen Sie: Sei 
ein Punkt und 
eine Gerade. Es existiert genau ein Lot von auf .
Auf drei Bildern eine mögliche Beweisidee:
| Beweisschritt (Bild 1 von 2) | Begründung (Bild 2 von 2) |
|---|---|
 |
|
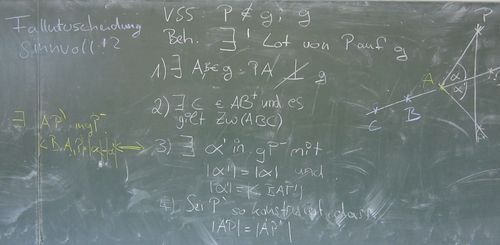Wir KÖNNTEN folgende Fälle unterscheiden:
- Punkt A liegt derart, dass
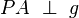gilt, dann wären wir fertig
- wir könnten auch den Fall annehmen, dass
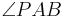so liegt, dass es der Außenwinkel von 
ist - dann müssten wir dies in unsere Beweisführung einplanen.
All das ist aber wohl nicht zielführend, da wir beweisen wollen, dass das Lot zunächst nur existiert. Unter der Vorraussetzung (und der Skizze) können wir ein Lot darstellen - somit sind wir fertig!
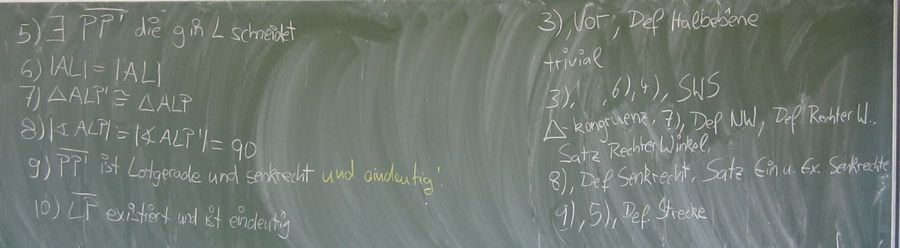
Wir haben die Eindeutigkeit des Lotes direkt gezeigt, man hätte es auch indirekt zeigen können! --Flo60 14:47, 15. Jul. 2012 (CEST)
