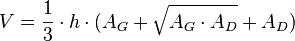Körpermodelle: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Tetraeder)
(→‎Mantelfläche)
 
Zeile 72: Zeile 72:
 
<math>A_M =\frac{3a^2}4\cdot \sqrt{3}</math>
 
<math>A_M =\frac{3a^2}4\cdot \sqrt{3}</math>
  
 +
==Oberfläche==
 +
<math>A_O={a^2}\cdot \sqrt{3}</math>
 +
 +
===Volumen===
 +
 +
<math>A_M =\frac{a^3}{12}\cdot \sqrt{2}</math>
  
 
<br><br>
 
<br><br>

Aktuelle Version vom 17. Juli 2012, 18:40 Uhr

Inhaltsverzeichnis

Aus dem Sommersemester 2012

Die folgenden Modelle wurden im Sommersemester 2012 von den Studierenden der Veranstaltung Erstellen von Multimediaanwendungen für den Unterricht generiert.

Ikosaeder

[ www.ph-heidelberg.de is not an authorized iframe site ]



Änderung der Drehrichtung: Ziehen mit der Maus über die App.

Wichtige Informationen zum Ikosaeder


Art der Flächen Gleichseitige Dreiecke
Anzahl der Flächen 20
Anzahl der Ecken 12
Anzahl der Kanten 30
Netz [1] ‎



Berechnungen am Ikosaeder

Seitenlänge a

Oberflächenberechnung:

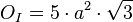
O_I=5\cdot a^2\cdot\sqrt{3}

Volumenberechnung:

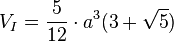
V_I=\frac{5}{12} \cdot a^3 (3+\sqrt{5})


Verwendung des Ikosaeders

In erster Lienie ist der Ikosaeder als 20-Seitiger Spielwürfel geläufig und ist in dieser Verwendung den meisten Schülern geläufig. Ein weiteres Beispiel für Ikosaeder finden sich bei den Capsiden vieler Viren, welche die Form von Ikosaeder annehmen. Ein in die Erdkugel platziertes Ikosaeder bildet den Kern der Gitterstruktur beim Wettervorhersagemodell GME des Deutschen Wetterdienstes. - siehe [2]


Wuerfel w20.jpg

--Aotearoa 14:05, 17. Jul. 2012 (CEST)

Oktaeder

[ www.ph-heidelberg.de is not an authorized iframe site ]

Änderung der Drehrichtung: Ziehen mit der Maus über die App.

6-seitiges Prisma

[ www.ph-heidelberg.de is not an authorized iframe site ]

Pyramide

Tetraeder

[ www.ph-heidelberg.de is not an authorized iframe site ]


Mantelfläche

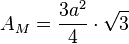
A_M =\frac{3a^2}4\cdot \sqrt{3}

Oberfläche

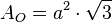
A_O={a^2}\cdot \sqrt{3}

Volumen

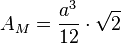
A_M =\frac{a^3}{12}\cdot \sqrt{2}



quadratische Pyramide

[ www.ph-heidelberg.de is not an authorized iframe site ]

Grundfläche

A_G=a^2

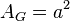
Mantelfläche

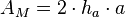
A_M =2\cdot h_a \cdot a

Oberfläche

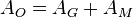
A_O =A_G+A_M

Volumen

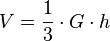
V= \frac{1}{3} \cdot G \cdot h




Pyramidenstumpf

quadratischer Pyramidenstumpf

[ www.ph-heidelberg.de is not an authorized iframe site ]

Grundfläche

A_G=a^2

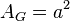
Deckfläche

A_D=b^2

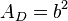
Mantelfläche

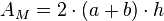
A_M =2 \cdot (a + b) \cdot h

Oberfläche

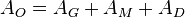
A_O =A_G + A_M + A_D

Volumen

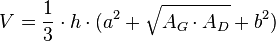
V= \frac{1}{3} \cdot h \cdot (a^2 + \sqrt{A_G\cdot A_D} + b^2) 

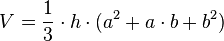
→ V= \frac{1}{3} \cdot h \cdot (a^2 + a \cdot b + b^2)




regelmäiger sechseckiger Pyramidenstumpf

[ www.ph-heidelberg.de is not an authorized iframe site ]

Grundfläche

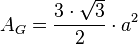
A_G=\frac{3\cdot\sqrt{3}}{2} \cdot a^2

Deckfläche

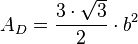
A_D=\frac{3\cdot\sqrt{3}}{2} \cdot b^2

Mantelfläche

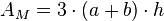
A_M =3 \cdot (a + b) \cdot h

Oberfläche

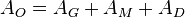
A_O = A_G + A_M + A_D

Volumen

V= \frac{1}{3} \cdot h \cdot (A_G + \sqrt{A_G\cdot A_D} + A_D)

Von „http://geometrie.zum.de/index.php?title=Körpermodelle&oldid=17283“