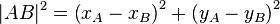Kreise 2012 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Abstände von Punkten) |
*m.g.* (Diskussion | Beiträge) (→Abstände von Punkten) |
||
| Zeile 21: | Zeile 21: | ||
=Abstände von Punkten= | =Abstände von Punkten= | ||
| − | <ggb_applet width=" | + | <ggb_applet width="1031" height="697" version="4.0" ggbBase64="UEsDBBQACAAIACxYWEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIACxYWEEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5Vr9bts4Ev+7+xSEbrFo0domRVEfrd1FEmCxBbLb4po79O56LSiJdrSRJVekE3tv+1D3IvdMNyQlRbIdx2m7zeIOqEtSHHJmfvPBoZTx96t5ji5FJbOymDhkiB0kiqRMs2I2cZZqOgid759/M56JcibiiqNpWc25mjiepszSiRNSHKYRjwcMT72BxxJ/wMM0GbAkimkoWDiNYgehlcyeFuXPfC7kgifidXIu5vy0TLgyjM+VWjwdja6uroYNq2FZzUazWTxcydRBIGYhJ07deQrb9RZdUUPuYkxGb346tdsPskIqXiTCQVqFZfb8mwfjq6xIyyt0laXqHBTGNHLQuchm56BUSFwHjTTVAhBZiERll0LC2s7QKK3mC8eQ8ULPP7A9lLf6OCjNLrNUVBMHD0kUUMwIJpiFAXB0UFllolA1Lal5jprdxpeZuLLb6p7h6DlIlWUec70j+u035GIXoye6IbZxofF9O4XtM0xt49rGsw2zNJ5d7llSz9J4lsYDGS8zmcW5mDhTnkuAMCumFZivHUu1zoWRp35wrT15AjrJ7Fcgphj8xGKu0cZP9M+Hn6cnRn0lSYerqpZ3ZNqwBITJ4Tzdz9KUNkxdzLZ5uuwGPf09TK3iBynKOtgCK/PP/LY40n1qbnK0489j6HtfRcXxqImVcR0eSJ5r2tp9lJhLHTA0QizSfk8Qg+DwA3BzhkgETeAiCAdEGPIYDEmIfN0GiAYw4SGKQqTpCEUmOlgI/3mB2cxHDDbTTwMISkSAkYcYRcQElYcglJAJTAhSlwIFY4jBIs2euHoL6iPPhxENkQcy6pgMCBBSWAhjYO8iShDVi0mAXB/5ej/i6Vj3Qy06bOkiHyOf6A0hrCGkbTgDfYio1sav4cqKxVL1IErmadNV5aK1BVBDQrpOezZB9bLig3HOY5HDSfFaWxKhS57riDCMpmWhUGPE0D6bVXxxniXytVAKVkn0C7/kp1yJ1Q9ALRvehjYpC/mqKtVJmS/nhUQoKXPcylzmpNN3W6lhQDsTXneCdSb8Tj/YybeEGbSUAviXlWzIeZq+0BTXqQGQfFnk6+NK8ItFmfXVGI/MoTMWyyTP0owXfwVn1Vw0LqhzBpHrM8inrJGkrNLXawkujFZ/F1UJARB5wwhCgtIIh57HIOWs7QxlZBi5AXZ9j9Aw9EKYkgnXwcfYkBIfB0FIPDdgzAdfWN80Z1mLy9ZEfCVa7WdVlnb7L+RxmactFkb9E75Qy8pUD5AbK63TUTHLhXERk23haE4u4nL12voGtXudrRcwwpZ/PDOwI0gNrlZyVrexbQ2NFqylwoYGGwrcOFuWtvMkcg2FaWPbGirwXitarShptCS4YZNJk9Cw0wsb4/r6nF8WmTptBipLLmpNiaX/eTmPRetA/S3JF9tSywwVh1Rv6hpO9//W6Z+dC8V1LcJcyqIwAFtHoRuFoXXTDQcdX4iqEHkdD+AIy3IpbXh3QiUVSTaHoZ2oAeXa2H8BBezTVMwq0eidm7rOwm1mcdfTtx6brX6oyvmL4vIMPGlDgPGokXIskypbaH9FMZwhF+LaJ0F3DkdQ2l2nAxigS/RRA/AqDS2E9lKdl5Wp3CAjQavjNhdzqNOQMs5p/Ls105EpALU9UBn/Aklxw4zXxoHpnY5qXJrni3NjmFrpnK9F1YPB7PdyOpVCoZUuNCB8J86AuJ3pn8q0xo402IFpjIKQPxamCAXnWQhh3c4qBJ0F8DPB2kuBYA5peA0tM6rbX6072fJYQ6EDuJfz7dMNO4JzWRRvwfP4nvAcmHwIOgS/P54DWgM6cL8UoqtFJaS+vDU4rd4fwRVuBTKuHh49sgd5H/diORdVljjdFebWwfNlzcdtxLoJa9xBmtwu1LoVan2gUOttoegXFmr1/rhF6vhApI43hRp8aanWrVTrA6Va75Dq8wyYlPM5L1JUmGr9ZQWZcVYWPD+F09K5LiM51mkQcajFVkdwqNUcl6qZlGBEs3W94ZYq+vht9ZDvd+TU5mpgSTpRdYhi+3PAdZDjrUAldaDiOk5bPK8LBgWl7AVc2KWpauoMgG3vxyxNRdFmD/GhsGukPciz+SLPkkx9Bu7HFvca4R7q8Xv3Dqhr6j8K6rhJj6SGfXAfuN+M9jbWyZ2wTnZh3TvlvhrUrIaaNUize0D6RaGgkAUUNuDWPnmje5/sB7xfVZx8UlWhX17MbBPb5s5lRWDQdaN9RcV2ofXF6oI+zq/KfA2JZLdTn0Dj7vJtuAvkcFUjloxbshgauGIntxnBMmxgbre63cF2+9edI4YwamzIyO7j7tCgubl8lWKmR60g/JNcbY+cB1ewzPgO8Q7zNbwR+QQfFvl3D3zjTbmuh9tAh0Jn+yJ5IcRC3/9fFmcVL6T+xGBpGsgON0L8dY2wB+Y2w+L/RZyTe3N2L7SZcu917doMjRUGjbsfeM79QazQz+PmTdruArzO4sdbWfw//96fqs1bltZuQL1xlSBDFuAg8qnrB5EXRr7/iRnZ1jAE33D/OCDGtt7ZHW44XiWdQ7R5wZTn5dWfxTQXK4PsnmDYuqadiZUi9UXtuw/LUj379rs/EfyMT+A6PYCLIpq8zcVUPbST6DF6eMrPxJt/wPQ/H8Gwfv7WvCJ9NLiJ+HgH8QTt2BQNUJ/67bO6s+sOqUB8p6/LfRammTR69A1Qf0SQcNmdtt+MzEtj7DQBWK+XilfqlS6KkEkS0TDyqMei0KckcFkU1Sde5PnEi2CMSRCyoFtq3W5ut29uUHkNpl5rU6Pd5lv3bL3f1Ou+8WpL79gRDN2nNX737R1sfb+XkN/B1sz1iI9D6oV+qD8orPXfJ0QeC3zfJWBsSjzvbramG7ZOJm/lh0r9i79zH8fv3I+oHm/ah3fsAqSb03Fv+iP4jdllK575u4fuow7t4y2KeIPi45arJJ3Zu3gH/T/wDrrhHexG9xh1vxaYL3r1n6c8/y9QSwcISQsSt6sIAAA7IwAAUEsBAhQAFAAIAAgALFhYQdY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAsWFhBSQsSt6sIAAA7IwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAEIJAAAAAA==" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "true" useBrowserForJS = "false" allowRescaling = "true" /> |
<br /><br /> | <br /><br /> | ||
Wir beziehen uns auf die obigen Punkte <math>A\left(x_A,y_A\right)</math> und <math>B\left(x_B,y_B\right)</math>.<br /> | Wir beziehen uns auf die obigen Punkte <math>A\left(x_A,y_A\right)</math> und <math>B\left(x_B,y_B\right)</math>.<br /> | ||
Version vom 24. Oktober 2012, 10:03 Uhr
Aufgaben zum Einstieg
Aufgabe 1Lassen Sie die folgenden Punktmengen in der obigen Geogebraapplikation grafisch darstellen. Um was für geometrische Objekte handelt es ich in jedem Fall? Begründen Sie Ihre Antwort. Aufgabe 2Lassen Sie die folgenden Kreise mittels Geoegebra grafisch darstellen, indem Sie jeweils eine entsprechende Gleichung in die Eingabezeile eintragen.
Kreise in der synthetischen GeometrieVereinbarungAlle unsere folgenden Betrachtungen beziehen sich auf die Geometrie in der Ebene. KreisdefinitionDefinition Es seien Abstände von Punkten
|
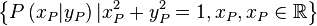
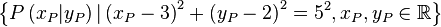
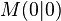 Radius:
Radius: 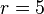
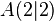 Radius:
Radius: 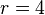
 ein Punkt und
ein Punkt und  eine positive reelle Zahl. Unter dem Kreis mit dem Mittelpunkt
eine positive reelle Zahl. Unter dem Kreis mit dem Mittelpunkt 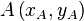 und
und 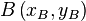 .
. ist der Schnittpunkt der Senkrechten durch
ist der Schnittpunkt der Senkrechten durch  auf die x-Achse mit der Senkrechten von
auf die x-Achse mit der Senkrechten von  auf die y-Achse.
auf die y-Achse.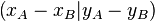 .
.
 ist rechtwinklig. Nach dem Satz des Pythagoras gilt:
ist rechtwinklig. Nach dem Satz des Pythagoras gilt: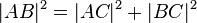
 schreibt sich (I) wie folgt:
schreibt sich (I) wie folgt: