Lösung Aufgabe 2.1 WS 12 13: Unterschied zwischen den Versionen
B..... (Diskussion | Beiträge) (→Lösung von User: ...) |
*m.g.* (Diskussion | Beiträge) (→Lösung von User: ...) |
||
| Zeile 26: | Zeile 26: | ||
| + | Und hier noch was zu schmunzel und warum es so wichtig ist sauber zu definieren. Viel Spaß | ||
| + | http://www.youtube.com/watch?v=3Fe-a2gUccs | ||
| + | |||
| + | |||
| + | a) Vor: Diagonalen halbieren sich<br />Beh: ABCD Parallelogramm | ||
| + | |||
| + | b)Vor: ABCD ist Parallelogramm<br />Beh: Diagonalen halbieren sich | ||
| + | |||
| + | c) Vor: ABCD ist kein Parallegramm<br />Beh: Diagonalen halbieren sich nicht | ||
| + | |||
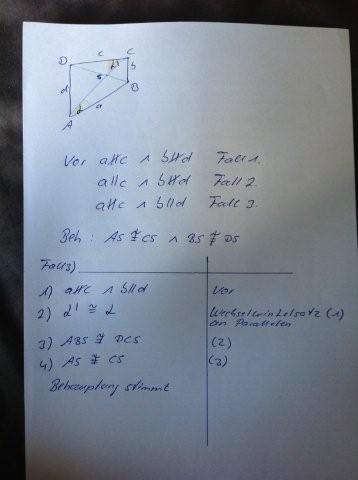
| + | d [[Bild:Foto (3).jpg]] | ||
| + | |||
| + | e)[[Bild:Foto (4) (2).jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | f)Wenn sich in einem Viereck die Diaganaolen halbieren genau dann ist es ein Parallelogramm<br />--[[Benutzer:Yellow|Yellow]] 11:14, 6. Nov. 2012 (CET) | ||
Version vom 6. November 2012, 23:34 Uhr
Aufgabe 2.1Der Begriff Parallelogramm sei als Viereck mit zwei Paaren paralleler Seiten definiert. Wir betrachten die folgende Implikation (I): (I) Wenn sich in einem Viereck die Diagonalen halbieren, dann ist das Viereck ein Parallelogramm. (a) Nennen Sie die Voraussetzung und die Behauptung der Implikation (I). Lösung von User: ...a: Vor.: Die Diagonalen eines Vierecks halbieren sich. Lösung von User: ...Und hier noch was zu schmunzel und warum es so wichtig ist sauber zu definieren. Viel Spaß http://www.youtube.com/watch?v=3Fe-a2gUccs
b)Vor: ABCD ist Parallelogramm c) Vor: ABCD ist kein Parallegramm
f)Wenn sich in einem Viereck die Diaganaolen halbieren genau dann ist es ein Parallelogramm
|