Lösung von Aufgabe 3.6 WS 12 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="background…“) |
Caro44 (Diskussion | Beiträge) (→Lösung von User ...) |
||
| Zeile 23: | Zeile 23: | ||
b) '''Beweisen Sie den Satz indirekt mit Widerspruch.'''<br /> | b) '''Beweisen Sie den Satz indirekt mit Widerspruch.'''<br /> | ||
| − | ==Lösung von User ...== | + | ==Lösung von User Caro44== |
| + | |||
| + | |||
| + | == a)== | ||
| + | |||
| + | '''Beweis 1:''' Der Beweis ist falsch, da hier nicht der Basiswinkelsatz, sondern die Kontraposition des Basiswinkelsatzes als Begründung herangezogen werden muss. | ||
| + | |||
| + | '''Beweis 2:''' Der Beweis ist richtig. Die Kontraposition der Umkehrung ist äquivalent zur Umkehrung des Basiswinkelsatzes, die ja bereits bewiesen wurde bzw. als Begründung herangezogen werden darf. | ||
| + | |||
| + | |||
| + | |||
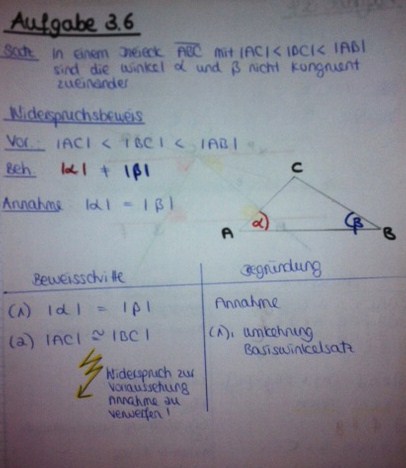
| + | == b) == | ||
| + | [[Datei:Caro44_Beweis_Basiswinkelsatz.JPG]] | ||
| + | |||
| + | --[[Benutzer:Caro44|Caro44]] 14:20, 14. Nov. 2012 (CET) | ||
==Lösung von User ...== | ==Lösung von User ...== | ||
Version vom 14. November 2012, 14:20 Uhr
|
Aufgabe 3.6Satz: In einem Dreieck Beweis 1) Lösung von User Caro44a)Beweis 1: Der Beweis ist falsch, da hier nicht der Basiswinkelsatz, sondern die Kontraposition des Basiswinkelsatzes als Begründung herangezogen werden muss. Beweis 2: Der Beweis ist richtig. Die Kontraposition der Umkehrung ist äquivalent zur Umkehrung des Basiswinkelsatzes, die ja bereits bewiesen wurde bzw. als Begründung herangezogen werden darf.
b)--Caro44 14:20, 14. Nov. 2012 (CET) Lösung von User ... |
 mit |AC|< |BC| < |AB| sind die Winkel α und β nicht kongruent zueinander.
mit |AC|< |BC| < |AB| sind die Winkel α und β nicht kongruent zueinander.