Lösung von Aufgabe 3.6 WS 12 13: Unterschied zwischen den Versionen

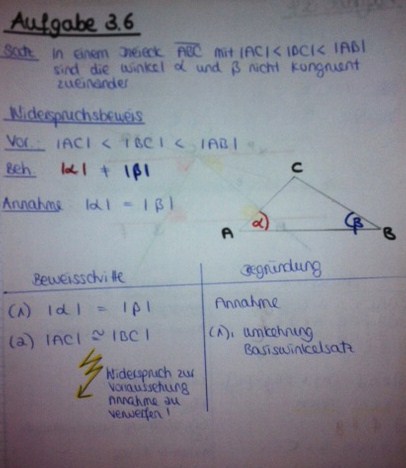
Aufgabe 3.6

Satz: In einem Dreieck mit |AC|< |BC| < |AB| sind die Winkel α und β nicht kongruent zueinander.

a) Welcher Beweis ist korrekt? Begründen Sie ausführlich! (Der Basiswinkelsatz und seine Umkehrung seien bereits bewiesen.)

Beweis 1)
Sei ein Dreieck.
Vor: |AC|< |BC| < |AB|.
Beh: |α| ≠ |β|
Bew: Da nach Voraussetzung |AC| ≠ |BC| gilt nach dem Basiswinkelsatz |α| ≠ |β|. Damit ist der Satz bewiesen.

Beweis 2)
Sei ein Dreieck.
Vor: |AC|< |BC| < |AB|.
Beh: |α| ≠ |β|
Bew: Nach Umkehrung des Basiswinkelsatzes gilt: Wenn |α|= |β| dann gilt |AC|= |BC|. Die Kontraposition der Umkehrung lautet also: Wenn |AC| ≠ |BC| dann gilt |α| ≠ |β|. Da die Kontraposition gleichwertig ist, kann man auch diese beweisen. Da nach Voraussetzung gilt: |AC|< |BC|, d.h. |AC| ≠ |BC|, kann nach Kontraposition der Umkehrung des Basiswinkelsatzes direkt gefolgert werden: |α| ≠ |β|. Damit ist der Satz bewiesen.

b) Beweisen Sie den Satz indirekt mit Widerspruch.

Lösung von User Caro44

a)

Beweis 1: Der Beweis ist falsch, da hier nicht der Basiswinkelsatz, sondern die Kontraposition des Basiswinkelsatzes als Begründung herangezogen werden muss.

Beweis 2: Der Beweis ist richtig. Die Kontraposition der Umkehrung ist äquivalent zur Umkehrung des Basiswinkelsatzes, die ja bereits bewiesen wurde bzw. als Begründung herangezogen werden darf.

zu Beweis 1: die Kontraposition des Basiswinkelsatzes ist doch: Winkel nicht gleich --> nicht gleichschenkliges Dreieck
Es müsste die Kontraposition von der Umkehrung sein, oder? --B..... 10:41, 15. Nov. 2012 (CET)

b)

--Caro44 14:20, 14. Nov. 2012 (CET)

Lösung von User ...