Vektorräume 2012 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Definition des Begriff des Vektorraums)
(→‎Definition des Begriff des Vektorraums)
Zeile 16: Zeile 16:
  
 
A3: Es gibt ein neutrales Element <math>e\in V</math>, mit dem für alle Elemente <math>u\in V</math> gilt: <math>u+ e = e+ u = u</math>. (Existenz eines neutralen Elements/Nullvektor) //<blockquote style="border: 1px solid blue; padding: 2em;">
 
A3: Es gibt ein neutrales Element <math>e\in V</math>, mit dem für alle Elemente <math>u\in V</math> gilt: <math>u+ e = e+ u = u</math>. (Existenz eines neutralen Elements/Nullvektor) //<blockquote style="border: 1px solid blue; padding: 2em;">
−
Ist das nicht bezüglich der Addition: also: u+e=e+u=u?
+
Ist das nicht bezüglich der Addition: also: u+e=e+u=u? <br />Sie haben Recht, ich hab es geändert.--[[Benutzer:*m.g.*|*m.g.*]] 11:32, 8. Dez. 2012 (CET)
 
</blockquote>A4: Zu jeden <math>u\in V</math> existiert ein Gegenvektor <math>-u \in V</math> mit<math>u+(-u)=e. </math>
 
</blockquote>A4: Zu jeden <math>u\in V</math> existiert ein Gegenvektor <math>-u \in V</math> mit<math>u+(-u)=e. </math>
  

Version vom 8. Dezember 2012, 11:32 Uhr

Definition des Begriff des Vektorraums

Eine nicht leere Menge V zusammen mit einer inneren Verknüpfung

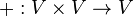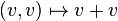
+: V \times V \to V, (v,v)\mapsto v+v

und der äußeren Verknüpfung

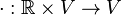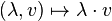
{\cdot}: \mathbb{R} \times V \to V, (\lambda ,v)\mapsto \lambda \cdot v

heißt reeler Verktorraum, falls folgende Bedingungen erfüllt sind:

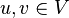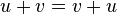A1: Für beliebige u,v \in V gilt u+v=v+u (Kommuntativität der Addition).

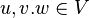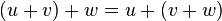A2: Für beliebige u,v.w \in V gilt (u+v)+w=u+(v+w). (Assoziativität der Addition)

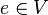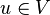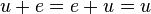A3: Es gibt ein neutrales Element e\in V, mit dem für alle Elemente u\in V gilt: u+ e = e+ u = u. (Existenz eines neutralen Elements/Nullvektor) //
Ist das nicht bezüglich der Addition: also: u+e=e+u=u?
Sie haben Recht, ich hab es geändert.--*m.g.* 11:32, 8. Dez. 2012 (CET)
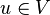A4: Zu jeden u\in V existiert ein Gegenvektor 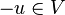-u \in V mitu+(-u)=e.

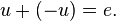
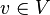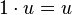S1: Für beliebige v \in V gilt 1\cdot u =u.

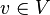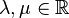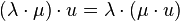S2: Für beliebige v \in V und beliebige \lambda, \mu \in \mathbb{R} gilt: (\lambda \cdot \mu)\cdot u= \lambda\cdot(\mu\cdot u) (Assoziativität der Multiplikation von Vektoren mit reelen Zahlen)

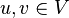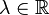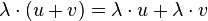S3: Für beliebige u,v \in V und beliebige \lambda \in \mathbb{R} gilt: \lambda \cdot (u+v)=\lambda \cdot u +\lambda \cdot v (1.Distributivgesetz)

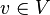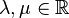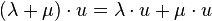S4: Für beliebige v \in V und beliebige \lambda, \mu \in \mathbb{R} gilt: (\lambda + \mu)\cdot u=\lambda \cdot u + \mu \cdot u (2.Distributivgesetz)

Bemerkung:

Die Eigenschaften A1-A4 lassen sich zusammenfassen, dass 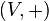(V, +) eine Abelsche Gruppe bildet.

Die Menge aller Pfeilklassen in der Ebene (und die Pfeilklassen des Raumes) mit den Eigenschaften, wie in der Vorlesung gezeigt, bilden einen Vektorraum.

(Quelle: Filler: Elementare Lineare Algebra. Spektrum Akademischer Verlag)

Von „http://geometrie.zum.de/index.php?title=Vektorräume_2012_13&oldid=19266“