Serie 7 (WS 12 13): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 7.7) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> | ||
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| + | |||
| + | <!--- ------------------------------------------------------------------------------------------ ---> | ||
| + | |||
=Ohne Axiom vom Lineal= | =Ohne Axiom vom Lineal= | ||
==Aufgabe 7.1== | ==Aufgabe 7.1== | ||
| Zeile 48: | Zeile 54: | ||
===Bemerkung=== | ===Bemerkung=== | ||
Unter ''fast allen'' versteht der Mathematiker ''alle bis auf endlich viele''. | Unter ''fast allen'' versteht der Mathematiker ''alle bis auf endlich viele''. | ||
| + | |||
| + | <!--- Das, was hier drunter steht muss stehen bleiben, also oberhalb dieses Kommentars Änderungen einfügen ---> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | |||
| + | [[Category:Einführung_S]] | ||
Version vom 8. Dezember 2012, 18:02 Uhr
|
Ohne Axiom vom LinealAufgabe 7.1Bauen Sie die folgende Applikation nach: Hilfen
Aufgabe 7.2Definieren Sie:
BemerkungDer Äquator und alle Längenkreise der Erdkugel sind Beispiele für Großkreise. Mit Axiom vom LinealFür die folgenden Aufgaben arbeiten Sie bitte Streckenmittelpunkte und das Axiom vom Lineal WS 12 13 durch. Aufgabe 7.3Welcher geometrische Begriff, den Sie aus der Schule kennen, wird im Folgenden beschrieben? Ebene Geometrie sei vorausgesetzt. Es seien Aufgabe 7.4Was ist in der folgenden Definition alles nicht korrekt? Definition Mittelpunkt einer Strecke
Aufgabe 7.5Beweisen Sie, dass jede Strecke einen Mittelpunkt hat. Aufgabe 7.6Beweisen Sie die Eindeutigkeit des Mittelpunktes einer Strecke. Aufgabe 7.7Es sei BemerkungUnter fast allen versteht der Mathematiker alle bis auf endlich viele. |
 . Die Strecke wird zunächst ganz normal generiert. Dann Rechtsklick auf das Objekt: Eigenschaften, Erweitert, Bedingung um Objekt anzuzeigen. Sie haben bereits AB, PB und PA berechnen lassen. Für das Anzeigen der Strecke AB geben Sie jetzt ein: PA+PB==AB. (Die beiden Gleichheitszeichen sind kein Tippfehler)
. Die Strecke wird zunächst ganz normal generiert. Dann Rechtsklick auf das Objekt: Eigenschaften, Erweitert, Bedingung um Objekt anzuzeigen. Sie haben bereits AB, PB und PA berechnen lassen. Für das Anzeigen der Strecke AB geben Sie jetzt ein: PA+PB==AB. (Die beiden Gleichheitszeichen sind kein Tippfehler)
 und dem Radius
und dem Radius 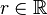 ,
,
 (Durchmesser und Radius sind als geometrische Objekte und nicht als Zahlen zu verstehen),
(Durchmesser und Radius sind als geometrische Objekte und nicht als Zahlen zu verstehen),
 und
und  zwei Punkte. Ferner sei
zwei Punkte. Ferner sei 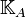 die Menge aller Kreise mit dem Mittelpunkt
die Menge aller Kreise mit dem Mittelpunkt 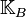 die Menge aller Kreise mit dem Mittelpunkt
die Menge aller Kreise mit dem Mittelpunkt 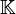 aller Kreise der Ebene sei die Funktion
aller Kreise der Ebene sei die Funktion 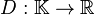 definiert, die jeden Kreis auf die Länge seiner Durchmesser abbildet.
definiert, die jeden Kreis auf die Länge seiner Durchmesser abbildet. 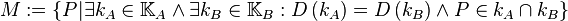
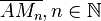 ist eine Folge von Strecken mit
ist eine Folge von Strecken mit 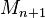 ist der Mittelpunkt von
ist der Mittelpunkt von 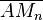 . Beweisen Sie: Für jedes
. Beweisen Sie: Für jedes 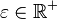 gilt: Fast alle Folgeglieder von
gilt: Fast alle Folgeglieder von  mit
mit 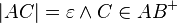 .
.

