Lösung von Aufgabe 7.7 WS 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="background…“) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 4: | Zeile 4: | ||
<!--- ------------------------------------------------------------------------------------------ ---> | <!--- ------------------------------------------------------------------------------------------ ---> | ||
| + | ==Aufgabe 7.7== | ||
| + | Es sei <math>\overline{AB}</math> eine Strecke. <math>\overline{AM_n}, n \in \mathbb{N}</math> ist eine Folge von Strecken mit <math>M_{n+1}</math> ist der Mittelpunkt von <math>\overline{AM_n}</math>. Beweisen Sie: Für jedes <math>\varepsilon \in \mathbb{R}^+</math> gilt: Fast alle Folgeglieder von <math>\overline{AM_n}</math> sind Teilmengen von <math>\overline{AC}</math> mit <math>|AC|=\varepsilon \wedge C \in AB^+</math>. | ||
| + | ===Bemerkung=== | ||
| + | Unter ''fast allen'' versteht der Mathematiker ''alle bis auf endlich viele''. | ||
Version vom 8. Dezember 2012, 18:14 Uhr
Aufgabe 7.7Es sei BemerkungUnter fast allen versteht der Mathematiker alle bis auf endlich viele.
Lösung von User ...Lösung von User ... |
eine Strecke. 
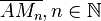ist eine Folge von Strecken mit 
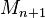ist der Mittelpunkt von 
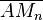. Beweisen Sie: Für jedes 
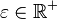gilt: Fast alle Folgeglieder von 
mit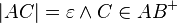 
.
