Gruppen, abelsche Gruppen 2012 12: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Gruppe der Deckabbildungen des Rechtecks)
(→‎Gruppe der Deckabbildungen des Rechtecks)
Zeile 33: Zeile 33:
 
Kommutative Gruppen werden auch Abelsche Gruppen genannt.
 
Kommutative Gruppen werden auch Abelsche Gruppen genannt.
 
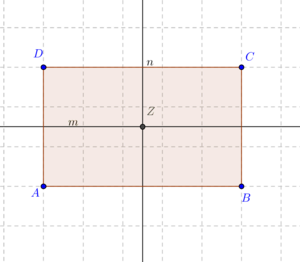
==Gruppe der Deckabbildungen des Rechtecks==
 
==Gruppe der Deckabbildungen des Rechtecks==
−
[[Bild:Decvkabbildungen_Rechteck.png|300px]]<br />
+
[[Bild:Decvkabbildungen_Rechteck.png| 300px]]<br />
 
Unter <math>D_R</math> wollen wir die Menge aller Bewegungen verstehen, die das Rechteck <math>\overline{ABCD}</math> auf sich selbst abbilden.  
 
Unter <math>D_R</math> wollen wir die Menge aller Bewegungen verstehen, die das Rechteck <math>\overline{ABCD}</math> auf sich selbst abbilden.  
  

Version vom 9. Dezember 2012, 18:27 Uhr


Beispiele für endliche Gruppen

Restklassen modulo 4

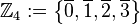
\mathbb{Z}_4:=\left\{ \overline{0}, \overline{1}, \overline{2}, \overline{3} \right\}
mit
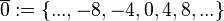\overline{0}:=\left\{..., -8, -4, 0, 4, 8, ...\right\} (Menge aller durch 4 teilbaren ganzen Zahlen),
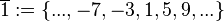\overline{1}:=\left\{..., -7, -3, 1, 5, 9, ...\right\} (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),
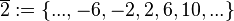\overline{2}:=\left\{..., -6, -2, 2, 6, 10, ...\right\} (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),
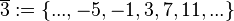\overline{3}:=\left\{..., -5, -1, 3, 7, 11, ...\right\} (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen),

Wir definieren auf \mathbb{Z}_4 eine Verknüpfung \oplus wie folgt:
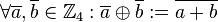
\forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a}\oplus \overline{b} := \overline{a+b}

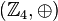Die Struktur \left(\mathbb{Z}_4, \oplus\right) ist eine Gruppe:

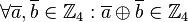  1. Die Verknüpfung \oplus ist auf der Menge \mathbb{Z}_4 abgeschlossen, d.h. \forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a} \oplus \overline{b} \in \mathbb{Z}_4,
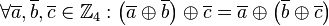  2. Die Verknüpfung \oplus ist auf der Menge \mathbb{Z}_4 assoziativ, d.h. \forall \overline{a}, \overline{b}, \overline{c} \in \mathbb{Z}_4: \left(\overline{a} \oplus \overline{b} \right) \oplus \overline{c}= \overline{a} \oplus \left( \overline{b} \oplus \overline{c} \right),
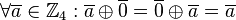  3. \mathbb{Z}_4 hat ein neutrales Element, nämlich die Klasse \overline{0}, d.h. \forall \overline{a} \in \mathbb{Z}_4: \overline{a} \oplus \overline{0}= \overline{0} \oplus \overline{a} = \overline{a},
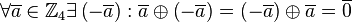  4. Zu jedem Element aus \mathbb{Z}_4 gibt es ein inverses Element, d.h. \forall \overline{a} \in \mathbb{Z}_4 \exist \left(-\overline{a}\right): \overline{a} \oplus \left(-\overline{a}\right) = \left(-\overline{a}\right) \oplus \overline{a} = \overline{0} .

Die folgende Verknüpfungstafel verdeutlicht die obigen Eigenschaften:



Die Tabelle wurde mit der Tabellenkalkulation von Geogebra generiert. Aus diesem Grunde fehlen die Querstriche über den Klassen.

Die Verknüpfungstabelle zeigt eine weitere Eigenschaft der Gruppe \left(\mathbb{Z}_4, \oplus\right):
Die Ergebnisse in der Tabelle sind symmetrisch bezüglich der Hauptdiagonalen angeordnet. Letzteres bedeutet, dass die Verknüpfung \oplus auf \mathbb{Z}_4 kommutativ ist:

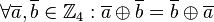  • \forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a} \oplus \overline{b} = \overline{b} \oplus \overline{a}.

Kommutative Gruppen werden auch Abelsche Gruppen genannt.

Gruppe der Deckabbildungen des Rechtecks

Decvkabbildungen Rechteck.png
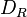Unter D_R wollen wir die Menge aller Bewegungen verstehen, die das Rechteck \overline{ABCD} auf sich selbst abbilden.

Von „http://geometrie.zum.de/index.php?title=Gruppen,_abelsche_Gruppen_2012_12&oldid=19403“