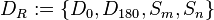Gruppen, abelsche Gruppen 2012 12: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Jessy* (Diskussion | Beiträge) (→Gruppe der Deckabbildungen des Rechtecks) |
Jessy* (Diskussion | Beiträge) (→Gruppe der Deckdrehungen des Quadrats) |
||
| Zeile 42: | Zeile 42: | ||
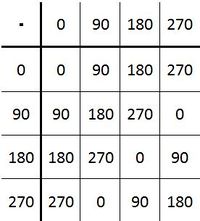
2. Assoziativität --> Drehungen sind immer assoziativ<br /> | 2. Assoziativität --> Drehungen sind immer assoziativ<br /> | ||
3. Neutrales Element: <math>D_{0}</math><br /> | 3. Neutrales Element: <math>D_{0}</math><br /> | ||
| − | 4. Inverse Elemente: <math>D_{0} \cdot D_{0}= D_{0}</math> und <math>D_{90} \cdot D_{270} = D_{0}</math> und <math>D_{180} \cdot D_{180} = D_{0}</math> und <math>D_{270} \cdot D_{90} = D_{0}</math> | + | 4. Inverse Elemente: <math>D_{0} \cdot D_{0}= D_{0}</math> und <math>D_{90} \cdot D_{270} = D_{0}</math> und <math>D_{180} \cdot D_{180} = D_{0}</math> und <math>D_{270} \cdot D_{90} = D_{0}</math><br /><br /> |
| − | Anmerkung: Die Gruppe der Deckdrehungen des Quadrats ist eine | + | Anmerkung: Die Gruppe der Deckdrehungen des Quadrats ist eine zyklische Gruppe.<br /><br /> |
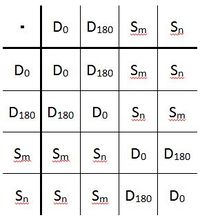
==Gruppe der Deckabbildungen des Rechtecks== | ==Gruppe der Deckabbildungen des Rechtecks== | ||
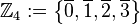
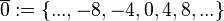 (Menge aller durch 4 teilbaren ganzen Zahlen),
(Menge aller durch 4 teilbaren ganzen Zahlen),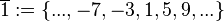 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),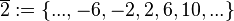 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),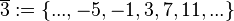 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen), eine Verknüpfung
eine Verknüpfung  wie folgt:
wie folgt: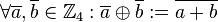
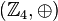 ist eine Gruppe:
ist eine Gruppe:
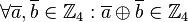 ,
,
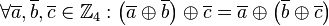 ,
,
 , d.h.
, d.h. 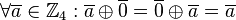 ,
,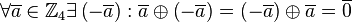 .
.
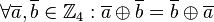 .
.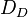 die Menge aller Drehungen die das Quadrat
die Menge aller Drehungen die das Quadrat  auf sich selbst abbilden:
auf sich selbst abbilden: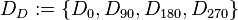
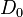
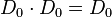 und
und 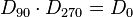 und
und 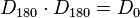 und
und 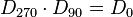
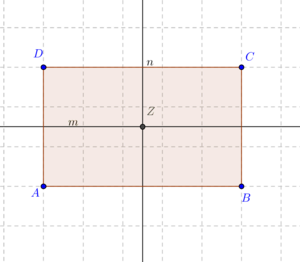
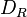 wollen wir die Menge aller Bewegungen verstehen, die das Rechteck
wollen wir die Menge aller Bewegungen verstehen, die das Rechteck  ) und Geradenspiegelungen:
) und Geradenspiegelungen: