Drehungen (2012 13): Unterschied zwischen den Versionen
Jessy* (Diskussion | Beiträge) (→Definitionsmöglichkeiten) |
Jessy* (Diskussion | Beiträge) (→Definitionsmöglichkeiten) |
||
| Zeile 14: | Zeile 14: | ||
Auch diese Definition basiert letztlich auf einem Kriterium:<br \> | Auch diese Definition basiert letztlich auf einem Kriterium:<br \> | ||
<u>Kriterium D2:</u> Eine BEwegung ist genau dann eine Drehung, wenn sie genau einen Fixpunkt besitzt.<br \><br \><br \> | <u>Kriterium D2:</u> Eine BEwegung ist genau dann eine Drehung, wenn sie genau einen Fixpunkt besitzt.<br \><br \><br \> | ||
| − | --[[Benutzer:Jessy*|Jessy*]] 13:48, 12. Dez. 2012 (CET) | + | --[[Benutzer:Jessy*|Jessy*]] 13:48, 12. Dez. 2012 (CET)<br \><br \><br \> |
| + | ==Drehungen als Bewegungen== | ||
| + | '''Satz 6.1'''<br \> | ||
| + | Jede Drehung ist eine Bewegung. | ||
Version vom 12. Dezember 2012, 13:53 Uhr
Definitionsmöglichkeiten
Definition 1
Unter einer Drehung 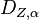 um den Punkt Z mit dem Drehwinkel
um den Punkt Z mit dem Drehwinkel  versteht man eine Abbildung
versteht man eine Abbildung  der Ebene
der Ebene  auf sich, für die gilt:
auf sich, für die gilt:
1. Z ist Fixpunkt bezüglich 
2. 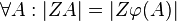 mit
mit 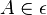 und
und 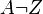
3. 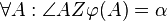 mit
mit 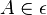 und
und 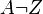
Die Definition entstand aus Vorüberlegungen.
Definition 2
Unter der Drehung 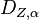 um den Punkt Z mit dem Drehwinkel
um den Punkt Z mit dem Drehwinkel  versteht man die NAF zweier Geradenspiegelungen
versteht man die NAF zweier Geradenspiegelungen 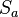 und
und 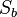 mit
mit 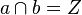 und
und 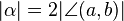
Dieser Definition liegt ein Kriterium zugrunde:
Kriterium D1: Eine Bewegung ist genau dann eine Drehung 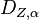 , wenn die die NAF zweier Geradenspiegelungen
, wenn die die NAF zweier Geradenspiegelungen 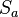 und
und 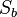 mit
mit 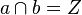 und
und 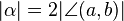 ist.
ist.
Definition 3
Unter einer Drehung vertseht man eine Bewegung mit genau einem Fixpunkt.
Auch diese Definition basiert letztlich auf einem Kriterium:
Kriterium D2: Eine BEwegung ist genau dann eine Drehung, wenn sie genau einen Fixpunkt besitzt.
--Jessy* 13:48, 12. Dez. 2012 (CET)
Drehungen als Bewegungen
Satz 6.1
Jede Drehung ist eine Bewegung.

