Serie 05 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 01) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 01) |
||
| Zeile 2: | Zeile 2: | ||
Es sei <math>\varphi \in \mathbb{R}</math>.<br /> | Es sei <math>\varphi \in \mathbb{R}</math>.<br /> | ||
Wir definieren die folgende Abbildung <math>f: \mathbb{R}^2 \rightarrow \mathbb{R}^2</math><br /> | Wir definieren die folgende Abbildung <math>f: \mathbb{R}^2 \rightarrow \mathbb{R}^2</math><br /> | ||
| − | <math>\forall \begin{pmatrix} x \\ y \end{pmatrix} \in \mathbb{R}^2: f \left( \begin{pmatrix} x \\ y \end{pmatrix}\right) = \begin{pmatrix}cos(\varphi) & -sin(\varphi) \\ sin(\varphi) & cos(\varphi) \end{pmatrix}\cdot \begin{pmatrix} x \\ y \end{pmatrix}= \begin{pmatrix} cos(\varphi)x + (-sin(\varphi))y \\ sin(\varphi)x + cos(\varphi) y \end{pmatrix}</math>. | + | <math>\forall \begin{pmatrix} x \\ y \end{pmatrix} \in \mathbb{R}^2: f \left( \begin{pmatrix} x \\ y \end{pmatrix}\right) = \begin{pmatrix}cos(\varphi) & -sin(\varphi) \\ sin(\varphi) & cos(\varphi) \end{pmatrix}\cdot \begin{pmatrix} x \\ y \end{pmatrix}= \begin{pmatrix} cos(\varphi)x + (-sin(\varphi))y \\ sin(\varphi)x + cos(\varphi) y \end{pmatrix}</math>.<br /> |
Beweisen Sie: <math>f</math> ist eine lineare Abbildung. | Beweisen Sie: <math>f</math> ist eine lineare Abbildung. | ||
Version vom 13. Dezember 2012, 16:21 Uhr
Aufgabe 01
Es sei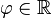 
.
Wir definieren die folgende Abbildung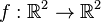 
.
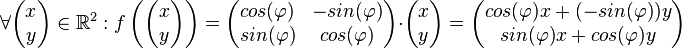Beweisen Sie: 
ist eine lineare Abbildung.
