Serie 05 12 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 5.2)
(→‎Aufgabe 5.2)
Zeile 10: Zeile 10:
  
 
=Aufgabe 5.2=
 
=Aufgabe 5.2=
−
Es sei <math>Z=\begin{pmatrix} 0 \\ 0 \\ d \end{pmatrix}</math>,<math>d \in \matbb{R}, d > 0</math>
+
Es sei <math>Z=\begin{pmatrix} 0 \\ 0 \\ d \end{pmatrix}</math>,<math>d \in \mathbb{R}, d > 0</math>

Version vom 15. Dezember 2012, 18:29 Uhr

Aufgabe 5.1

Es sei 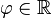\varphi \in \mathbb{R}.
Wir definieren die folgende Abbildung 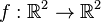f: \mathbb{R}^2 \rightarrow \mathbb{R}^2
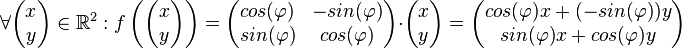\forall \begin{pmatrix} x \\ y \end{pmatrix} \in \mathbb{R}^2: f \left( \begin{pmatrix} x \\ y \end{pmatrix}\right) = \begin{pmatrix}cos(\varphi) & -sin(\varphi) \\ sin(\varphi) & cos(\varphi) \end{pmatrix}\cdot \begin{pmatrix} x \\ y \end{pmatrix}= \begin{pmatrix} cos(\varphi)x + (-sin(\varphi))y \\ sin(\varphi)x + cos(\varphi) y \end{pmatrix}.
Beweisen Sie: f ist eine lineare Abbildung.
Interpretieren Sie f geometrisch.
Hilfe:

Aufgabe 5.2

Es sei 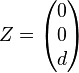Z=\begin{pmatrix} 0 \\ 0 \\ d \end{pmatrix},d \in \mathbb{R}, d > 0

Von „http://geometrie.zum.de/index.php?title=Serie_05_12_13&oldid=19738“