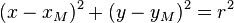Lösungen zu den Aufgaben 1: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(lösungen)
 
(→‎1.3)
 
Zeile 5: Zeile 5:
  
  
−
==2.2==
+
==1.2==
  
 
<math>3=5m+n</math><br />
 
<math>3=5m+n</math><br />
 
<math>2=2m+n</math><br />
 
<math>2=2m+n</math><br />
 
<math>\Rightarrow y=\frac{1}{3}+\frac{4}{3}</math>
 
<math>\Rightarrow y=\frac{1}{3}+\frac{4}{3}</math>
 +
 +
==1.3==
 +
Der Kreis <math>k</math> mit dem Mittelpunkt <math>M=(x_M;y_M)</math> und dem Radius <math>r</math> ist die Menge aller Punkte <math>P(x;y)</math> der Ebene, für die folgende Gleichung erfüllt ist: <br />
 +
<math>(x-x_M)^2+(y-y_M)^2=r^2</math>

Aktuelle Version vom 20. Dezember 2012, 16:06 Uhr

1.1

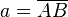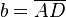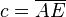Seien die Seitenlängen des Quaders a=\overline{AB}, b=\overline{AD} und c=\overline{AE}.
Die Diagonale 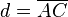d=\overline{AC} der Grundfläche ABCD ist damit 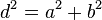d^2=a^2+b^2. Daraus ergibt sich die Raumdiagonale 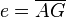e=\overline{AG} wie folgt: 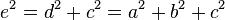e^2=d^2+c^2=a^2+b^2+c^2. (Pythagoras!)


1.2

3=5m+n
2=2m+n
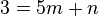
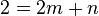
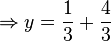
\Rightarrow y=\frac{1}{3}+\frac{4}{3}

1.3

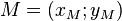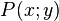Der Kreis k mit dem Mittelpunkt M=(x_M;y_M) und dem Radius r ist die Menge aller Punkte P(x;y) der Ebene, für die folgende Gleichung erfüllt ist:
(x-x_M)^2+(y-y_M)^2=r^2

Von „http://geometrie.zum.de/index.php?title=Lösungen_zu_den_Aufgaben_1&oldid=19835“