Geraden 2012 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Definition des Normalenvektors)
(→‎Definition des Normalenvektors)
Zeile 8: Zeile 8:
  
  
−
<ggb_applet width="206" height="47"  version="4.2" ggbBase64="UEsDBBQACAgIACSCKUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIACSCKUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vndktu2Fb52ngLDi16tJPyTdCVn7J3JNJl16sm6mUynNxCJlZClSIaEftZ13iYv0GfofZ+pBwCpX2u9u04dT3etBUEcnIPznYMPB/L4682iQCvdtKYqJxEZ4gjpMqtyU84m0dLeDJLo6xdfjWe6mulpo9BN1SyUnUR8SKPdPOgNCXOTTT6JZKoJ5iQfxHIqBlxzOVAEk0EypSkniWYM6wihTWuel9X3aqHbWmX6OpvrhbqqMmW9zrm19fPRaL1eD3vrw6qZjWaz6XDT5hGClZftJOoenoO6g0lr5sUpxmT00+uroH5gytaqMgP7zqulefHVs/HalHm1RmuT2zlgQJMkQnNtZnPwM3WdkZOqwdlaZ9asdAtz97reabuoIy+mSjf+LDyhYutPhHKzMrluJhEeEiFonArMCBYixVhEqGqMLm0nTDqjo17deGX0Ouh1T94kx2kMQTCtmRZ6Et2oogW/THnTAKawomYJ3dbeFXqqmr6/WxC5gF8QMO+00wXBC0BMIpriC0rERYzxhRA4rGXfcIRsVRVeK0YiRe/fI4opRheuIaGh0EgZhnB4h1loaGh4aESQ4WE6D6I8yPAgw9k9fnb9naPdiwNPez/Zvp8E/HMfCR8PwJGfyZ6fxDnxHhG3et8w5NZN/Ppdw7uuDN3YNwSHhnSDifvj8ZKf6BF7kkdkz2rIh/NGT/Klt0iw5A83SR9h8sTPrZf0Q15SccbLTwR366jYMwq2/D//OTHJ6GNMnof24RZdDJ6+959gMMafw+B41DPduNt7qJ072S53rF60jnVY6okHESRgY8oYeEIgkkITuw1KERGIC+iSBEnXxoi5PckRQwlycoQhTy8igT/c71eJBOhyL+OwcRHjSDBEPClxBFSEPLEByVEGEkIgAZOcdeLMMom4hA5LEIcFOkqLHW0wmAd9ME4RI4i5uSRGVCJJUexokXDHljJxawelFEmMpJsKvAicGPgQZiSIOW8gw+uqNVtw57qot1HxOJqyXtoD7LJF3j/a6kg6r7LbV0dYa9Xa/hmE4DDanXnhcDo4Ep+NCzXVBVQO1y4NEFqpwu1gr/+mKi3qU4CGd7NG1XOTtdfaWpjVop/VSl0pqzffgHTbL9Cb9kf1WC+zwuRGlT9CjjgVTiHantyel/qTOyGd6ayqmvz6roXMQZu/66aaRAOKxZDFAvOUkoTHIoED+C6MMZIMWSo5IyxOWMoA6TZTLueTeChxLAWHczGV0k05N+IN69XWM7XRW3/QrHHbaa/zbfuqKnav6sqU9lLVdtn4MgxIsHE+vSxnhfbYelaFgia7nVab6wAqC7re3tXQw2EF09llVVQNgg1JBax31rXT0HoZt7StFPYy2EvgPkom346TlHoJ305D66Ug7GFpnaukd5Pg3oxpPY2A8pBkPe+6pHHl0bI09qrvWJPddq6SMOH75WIK+dYl5KFO8nvpHI+OUmx8q5tSFyGPSgjmslq2IbO32flsvGz1G2XnL8v8Bz2DLflGOVa0oDqI7pac68wsYGJ434GnXGD/BksNb3M9a3TvYuEr3wCtH8X7WX3y2qv6pqkW35art5A1R0sdj3p/xm3WmNplJ5oCTd/qXf7lplVA8vn+PHC+BS8yRzgApHUgRkgt7bxqfG0L2xaqZfTdv38rS90AUUJCuh1b6AWUtcj6tPSZvQ3PS18wuzigavoz8Mj22AjjewDD+Adz1GezKuq5clV1h0Gh7mAF+6h4ha+r/BgrCIV3CLihDklRax3yKSwYHmpQ57fh3nI8+C3aOKMcOOfOPUhginfhDhUuDM5ZtzkPiDC8PYobpF3A6SOIvTpF7DDjd4n2xSLGh0J6xNiQ/C6AZdViococlb4QuQIiinbnn8Iuz5AiDrwAzNL2Ayqo6hScYO84bYus+vRkxU8HfgffgPYZx4eEpPs/Hs0BGUoOd8rdT3zM0BYO3Vu4Vrb+GLHdgeEf/mLyXPuKIpxgv5RhShto0yzqwmTG3h+CvzbACrOqVMX5YKiTYEwfEYzpx/bBZ4vGB4Jwtw3SO5fknLJ9Cfm5o/HGM8hhEKYn6F/ej/4hDV0+jYYIDSWIb78EKhrgYSrSJKWCMcJjylncMROmUB3SVIoEw72W8P8BUflq7iguKmyO0/D851/3x8cf+1v4Qdp/ZaSKZbcWMhQxjlPJqIxTnkCNGkyc57P7ThKCT7cQeWD4yD35z8/kf18mNdkOdLeGrkIqqvUP+qbQGw/pYcV1Hv8fweeq+TA7XZ4EYHk//qugrAdv+aUcFgSuMgcJHo5eOmTyIMGpT/CdpSew015B2vFTphqrWyilu1yz0PdshPSmdlgfVz6bugFLbk93OL3VGwu72Iv/6ZdlZf/8D0D6n+WvoeMVHAYCLo87ngrT/8hQmPZKvdU/Hd8C/G241Y252X5zAon92gUGR7tbcg8kPgGwYy8Bt07OsYBYShK7GT64KU/dNo+JZGnivsDekdfH8aYHeM8ejjT9Q5Heh7T/vu3xmLJhihPMATvAL2VE9IhKnCRxzGMmqBTkcYiyA0RfPhxR9n+AKCQpiVPGYyEEIZx3SQr3JiI4T3DMJGYYU3kO09H+1dN/FdT9b9CL/wJQSwcI5sGVTKAHAAC9GgAAUEsBAhQAFAAICAgAJIIpQtY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAAkgilC5sGVTKAHAAC9GgAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAADcIAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
+
<ggb_applet width="1269" height="860"  version="4.2" ggbBase64="UEsDBBQACAgIAEeCKUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAEeCKUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vndcty2Fb52ngLDi15JXPyTdFfO2JrJNBk59URuJtPpDZaEdhFxSYbE/sh13iYv0GfofZ+pBwC5v15ZllLHU0m7IMiDc3C+c/AdgBp/vZ6XaKnbztTVRURiHCFd5XVhqulFtLA352n09YuvxlNdT/WkVeimbufKXkQ8ptF2HPRiwtxgU1xEMtMEc1KcJ3Iizrnm8lwRTM7TCc04STVjWEcIrTvzvKq/V3PdNSrX1/lMz9VVnSvrdc6sbZ6PRqvVKh6sx3U7HU2nk3jdFRGCmVfdRdRfPAd1e4NWzItTjMnop9dXQf25qTqrqhzsO68W5sVXz8YrUxX1Cq1MYWeAAU3TCM20mc7Az8x1Rk6qAWcbnVuz1B2M3el6p+28ibyYqtzzZ+EKlRt/IlSYpSl0exHhmAhBk0xgRrAQGcYiQnVrdGV7YdIbHQ3qxkujV0Gvu/ImOc4SCILpzKTUF9GNKjvwy1Q3LWAKM2oX0O3sXaknqh362wmRM/gFAfNOO10QvADERUQzfEaJOEswPhMCh7nsGo6QrevSa8VIZOj9e0QxxejMNSQ0FBopwyMc7mEWGhoaHhoRZHgYzoMoDzI8yHB2j599f+tof2PP08FPtusnAf/cR8LHA3DgZ7rjJ3FOvEfEzd43DLl5Ez9/1/C+K0M38Q3BoSH9w9R9ebzkEz1ij/KI7FgN+XDa6FG+DBYJldnDTdInObpxk37ITSpOuPlEdDeeih2jYMv/+c+RSfZJfp7G9uEWJX/K4n+EwQR/DoPj0UB1437xoW7mZPt8tXreOdphmWceRJCAlSkTIAqBSAZN4lYoRUQgLqBLUiRdmyDmFiVHDKXIyRGGPL+IFL64X7ASCdDlbiZh5SLGkWCIeFbiCLgIeWYDlqMMJIRAAgY568SZZRJxCR2WIg4TdJyWON5gMA76YJwiRhBzY0mCqESSosTxIuGOLmXq5g5KKZIYSTcUiBFIMRAijEgRc95Ahjd1ZzbgznTZbKLicTRVs7B72OXzYri09YF0Uee3rw6w1qqzwzUIQTXaFr1QnfZq4rNxqSa6hK3DtUsDhJaqdCvY67+pK4s2BBLuTVvVzEzeXWtrYVSHflZLdaWsXn8D0t0wQW/a1+qxXuSlKYyqfoQccSqcQrQt3Y6YhtKdst5MXtdtcX3XQeag9d91W0MFY2ksE5xikhCW0gTq6F14IpmImRQ0FYzLlDKoAV2uXMYTKeOUU54kJEs4lVCz7048SoJhvdx4ptZ64w+atm457XS+7V7V5fZWU5vKXqrGLlq/DwMSbJ1PL6tpqT22nlZhR5PfTur1dQCVBV1v7xro4TCDyfSyLusWwYKkAiY87dtJaL2Mm9pGCnsZ7CXwECVTbJ6TjHoJ305C66Ug7GFqvatkcJPgwYzpPI2A8pBkA++6pHH7o0Vl7NXQsSa/7V0lYcD3i/kE8q1PyH2d5PfSOR4dpNj4VreVLkMeVRDMRb3oQmZvsvPZeNHpN8rOXlbFD3oKS/KNcqxoQXUQ3U650LmZw8BwvwdPucD+DaYa7hZ62urBxdJvfQO0/inezeqj217VN209/7ZavoWsOZjqeDT4M+7y1jQuO9EEaPpWb/OvMJ0Cki92x4HzHXiRO8IBIK0DMUJqYWd16ze3sGxhu4y++/dvVaVbIEpISLdiSz2HfS2yPi19Zm/C89LvmF0cUD35GXhkUzbC8x2A4fkHc9RnsyqbmXLb6h6DUt3BDHZR8Qpf18UhVhAK7xBwQxOSotE65FOYMFw0oM4vw53pePA7tHZGOdThO3chgZPfhUNUODE4Z93i3CPCcPcgbpB2AaePIPbqGLH9jN8m2heLGI+F9IixmPwugOX1fK6qAlV+I3IFRBRt65/CLs+QIg68AMzCDg9UUNUrOMLecdoGWfX0ZMWPB34L3zkdMo7HhGS7Px7NcxJLDofK7U9yyNAWiu4tnCs7X0ZsXzD8xV9MUWi/owgV7JcqDOkCbZp5U5rc2PtD8NcWWGFaV6o8HQx1FIzJJwRj8rF18Nmi8YEg3G2C9M4lOadsV0J+7mi88QyyH4TJEfqX96O/T0OXj6MhQsMWxLdfAhWd4zgTWZpRwRjhCeUs6ZkJU5YImkmRYjjYEv4/ICq/mzuIiwqL4zg8//nX/fHxZX8DP0j7d0aqXPRzIbFIcJJJBpvTjKeZ7NPwNJ/dV0kIPl5C5IHhI/fkPz+R/8M2qc23oLs59Duksl79oG9KvfaQ7u+4TuP/I/hctx9mp8ujACzux38ZlA3gLb6UYkFilu0leCi9FM44ewlOfYJvLT2CnXY2pD0/5aq1uoOtdJ9rFvqejZBeNw7rw53PumnBklvTPU5v9drCKvbif/plUds//wOQ/mf1a+h4BfuBgMPjlqfC8D8yFKa7Um/1T4enAH8a7nRrbjZvTiCxX7vA4O1rtmgAEh8B2LOXkDjhHAuIpYSjLO2Dm/HMLfOESJal7g32lrw+jjfdw3v6cKTpH4r0LqTD+7ZPx5TGRCRpJqTASZpm7hDjICVx6l7mwjk/o3DET5JPxJTtYfry4Ziy/wNMIU1JkjGeCCEI4bxPUzg5EcF5ihMmMcOYylOYjnYPn/5lUP8PoRf/BVBLBwjEevR/ogcAAMAaAABQSwECFAAUAAgICABHgilC1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAEeCKULEevR/ogcAAMAaAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAOQgAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Version vom 9. Januar 2013, 16:18 Uhr

Der Normalenvektor

Definition des Normalenvektors

Sei g eine Gerade und A ein Punkt auf dieser Geraden. Ein Vektor 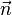\ \vec{n} \ heisst Normalenvektor von g am Aufpunkt A genau dann, wenn folgendes gilt:

i) 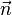\ \vec{n}\ steht senkrecht auf der Gerade g

ii) A \in \vec{n}


Von „http://geometrie.zum.de/index.php?title=Geraden_2012_13&oldid=20071“