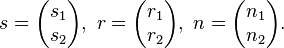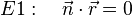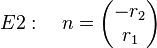Geraden 2012 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Definition des Normalenvektors) |
K (→Eigenschaften des Normalenvektors) |
||
| Zeile 15: | Zeile 15: | ||
=== Eigenschaften des Normalenvektors === | === Eigenschaften des Normalenvektors === | ||
| − | Sei g eine Gerade mit <math> \ \ g = \vec{s} + \lambda \cdot \vec{ | + | Sei g eine Gerade mit <math> \ \ g = \vec{s} + \lambda \cdot \vec{r} \ </math> und <math> \vec{n}</math> der Normalenvektor auf g , mit <math> s =\begin{pmatrix} s_1 \\ s_2 \end{pmatrix}, \ r =\begin{pmatrix} r_1 \\ r_2 \end{pmatrix},\ n =\begin{pmatrix} n_1 \\ n_2 \end{pmatrix}. </math> |
| − | E1: | + | <math> E1:\ \ \ \vec{n} \cdot \vec{r} = 0 </math><br><br> |
| + | <math> E2:\ \ \ n =\begin{pmatrix} -r_2 \\ r_1 \end{pmatrix} | ||
Version vom 9. Januar 2013, 17:29 Uhr
Der Normalenvektor
Definition des Normalenvektors
Sei g eine Gerade und A ein Punkt auf dieser Geraden. Ein Vektor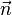 
heisst Normalenvektor von g am Aufpunkt A genau dann, wenn folgendes gilt:
i) 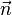steht senkrecht auf der Gerade g
ii)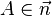 
Skizze eines Normalenvektors
Eigenschaften des Normalenvektors
Sei g eine Gerade mit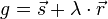 
und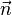 
der Normalenvektor auf g , mit 
