Lösung von Aufgabe 7.9: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 1: Zeile 1:
 
Definieren Sie mittels des Schnitts geeigneter Halbebenen den Begriff des Inneren eines Dreiecks <math>\overline{ABC}</math>.
 
Definieren Sie mittels des Schnitts geeigneter Halbebenen den Begriff des Inneren eines Dreiecks <math>\overline{ABC}</math>.
  
−
<math>\overline{AB}</math> = g
+
1)<math>\overline{AB}</math> = g
  
 
gC <math> \ OA^+ \ </math> := {P| Punkt, der links von g liegt}
 
gC <math> \ OA^+ \ </math> := {P| Punkt, der links von g liegt}
Zeile 8: Zeile 8:
  
  
−
:<math>\overline{ABC}</math> sei ein Dreieck und <math>\ a,b,c</math> drei Geraden mit <math>\overline{BC} \subset a, \ \ \overline{AC} \subset b, \ \ \overline{AB} \subset c</math>. Die Punktmenge <math>I = aA^+ \cap bB^+ \cap cC^+ \setminus \overline{ABC}</math> heißt das Innere des Dreiecks <math>\overline{ABC}</math>.
+
2):<math>\overline{ABC}</math> sei ein Dreieck und <math>\ a,b,c</math> drei Geraden mit <math>\overline{BC} \subset a, \ \ \overline{AC} \subset b, \ \ \overline{AB} \subset c</math>. Die Punktmenge <math>I = aA^+ \cap bB^+ \cap cC^+ \setminus \overline{ABC}</math> heißt das Innere des Dreiecks <math>\overline{ABC}</math>.
 
:--[[Benutzer:Sternchen|Sternchen]] 17:20, 10. Jun. 2010 (UTC)
 
:--[[Benutzer:Sternchen|Sternchen]] 17:20, 10. Jun. 2010 (UTC)
 +
 +
3)Gegeben seien drei nicht kollineare Punkte A, B und C. Die Schnittmenge der offenen Halbebenen ACB<sup>+</sup>, BCA<sup>+</sup> und ABC<sup>+</sup> heißt das Innere des Dreiecks <math>\overline{ABC}</math>.

Version vom 17. Juni 2010, 11:09 Uhr

Definieren Sie mittels des Schnitts geeigneter Halbebenen den Begriff des Inneren eines Dreiecks \overline{ABC}.

1)\overline{AB} = g

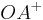gC \ OA^+ \  := {P| Punkt, der links von g liegt}

--Nicola 13:48, 6. Jun. 2010 (UTC)


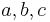2):\overline{ABC} sei ein Dreieck und \ a,b,c drei Geraden mit 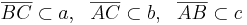\overline{BC} \subset a, \ \ \overline{AC} \subset b, \ \ \overline{AB} \subset c. Die Punktmenge 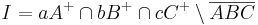I = aA^+ \cap bB^+ \cap cC^+ \setminus \overline{ABC} heißt das Innere des Dreiecks \overline{ABC}.

--Sternchen 17:20, 10. Jun. 2010 (UTC)

3)Gegeben seien drei nicht kollineare Punkte A, B und C. Die Schnittmenge der offenen Halbebenen ACB+, BCA+ und ABC+ heißt das Innere des Dreiecks \overline{ABC}.

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_7.9&oldid=2008“