Lösung von Aufg. 10.5 WS 12 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Lösung von User ...) |
|||
| Zeile 21: | Zeile 21: | ||
=Lösung von User ...= | =Lösung von User ...= | ||
Die Mittelsenkrechte einer Strecke ist die Menge aller Punkte, die zu den Endpunkten der Strecke ein und denselben Abstand. --LilPonsho 12:56, 20. Jan. 2013 (CET) | Die Mittelsenkrechte einer Strecke ist die Menge aller Punkte, die zu den Endpunkten der Strecke ein und denselben Abstand. --LilPonsho 12:56, 20. Jan. 2013 (CET) | ||
| − | + | ==Bemerkung --[[Benutzer:*m.g.*|*m.g.*]] 15:56, 20. Jan. 2013 (CET)== | |
| + | Besser: ..., die zu den Endpunkten der Strecke ''jeweils'' ein und denselben Abstand hat. (Ansonsten ließe es sich so interpretieren, dass der Abstand für alle Punkte immer derselbe sein müßte. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
Version vom 20. Januar 2013, 15:56 Uhr
--
Aufgabe 10.5Erläutern Sie, wie und warum sich aus den Satz VII.6 eine neue Möglichkeit, der Definition des Begriffs der Mittelsenkrechte ergibt. Lösung von Mr. Private 15:10, 19. Jan. 2013 (CET)Sei = Nach Axiom I.1 bildet P, Q eine Gerade g. Die Gerade g ist die Mittelsenkrechte der Strecke Bemerkung --*m.g.* 17:10, 19. Jan. 2013 (CET)Das beantwortet die Frage noch nicht ganz. Lösung von User ...Die Mittelsenkrechte einer Strecke ist die Menge aller Punkte, die zu den Endpunkten der Strecke ein und denselben Abstand. --LilPonsho 12:56, 20. Jan. 2013 (CET) Bemerkung --*m.g.* 15:56, 20. Jan. 2013 (CET)Besser: ..., die zu den Endpunkten der Strecke jeweils ein und denselben Abstand hat. (Ansonsten ließe es sich so interpretieren, dass der Abstand für alle Punkte immer derselbe sein müßte. |
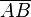 eine Strecke.
P und Q sind paarweise verschiedene Punkte.
eine Strecke.
P und Q sind paarweise verschiedene Punkte. 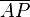 = Fehler beim Parsen(Lexikalischer Fehler): \overline{PB}\ \wedge \ \overline{AQ}
= Fehler beim Parsen(Lexikalischer Fehler): \overline{PB}\ \wedge \ \overline{AQ}
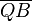 .
.
 .
.

