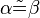|
|
| Zeile 8: |
Zeile 8: |
| | == Stufenwinkel, Wechselwinkel, entgegengesetzt liegende Winkel == | | == Stufenwinkel, Wechselwinkel, entgegengesetzt liegende Winkel == |
| | | | |
| − | In welchen Fällen handelt es sich um....
| + | Zeichnen Sie Bespiele und Gegenbeispiele zu den in der Überschrift genannten Begriffen und laden Sie die Bilder hier hoch. |
| − | ::Stufenwinkel
| + | |
| − | ::Wechselwinkel
| + | |
| − | ::entgegengesetzt liegende Winkel?
| + | |
| − | <ggb_applet width="1066" height="509" version="3.2" ggbBase64="UEsDBBQACAAIAKyt7DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VrdUts4FL7efQpPrnYvMPqXPAPttNACpbvd2e72Ym86TiwSbx07azv8vVVbnqPPtEeSE+LEBAwBAhlmTKRjWfq+cz7pnHjr5ekw8Y51XsRZut3BPup4Ou1lUZz2tzvj8mhDdV6++Hmrr7O+7uahd5Tlw7Dc7lCfdEz7OH7x809bxSA78cLEmnyK9cl25yhMCt3xilGuw6gYaF3W2sPxaZzEYX72ofuv7pXFZYcb5CAdjeEpZT6Gtt4weh8Xk6+b9oGjJC534+M40rmXZL3tjuAwdfjvk87LuBcm2x2GXAuBdUla64QmanoHWR6fZ2lpzC8HP4IWzyvicw13CtO2tWkXuqXHvSSO4jA1i7HzACPPO4mjcgC2VAgYU8f9AUxWIOmG62VZHn08K0o99E7/0Xm23SEE+wFHgUCcM86lkh3vzHVRFPgUE8URdFCBFYAIM4apMOEjjngAf7A0TDCDm67us8/Wxx91WQKZhRee6kuY+3kcTeA1/x8Ur7MkmnaPsjgtd8JROc6tI9Cq6WN5Zp4GyOVmka/SfqKrNgI8DXTvSzc7/eiQo27ov85G9hY7n25/J0uy3MvhBs7BoLp23dXamIlOrZC1QdaiGsMMOu3HAbEW9tp1V2uVxKmbWrVwPFk0RpPHxIVnGmBw47/TxSdhV4M/dLxxGpfvJ1/Ab75US8Xuht/Hwy4EzqznTMfEqxpza3PO57a+6DzViXOsFKgdZ+PCOzYe7J5lJxLpXjyEr66jgiQ0dP0NE3Ctke7nejJxF3YOMNuLZp13rnlrczIJM4cC5torQT9gPaVZiwnvEkJru7Ov4/T8OEz1uK/TjheFpek2gZTooYYoK61zWN+agvSqM5WUzKrDPIqXeEN/o6dYnwqT0SCEFr9aShKegVjMLs6O91sW1ZccpgCdXQ+E7MgMYMgZaR1VAllWHu2NYEgbHzPIW8AK79Q92DuD2DTXc3evNXGhZJTDPpZWPDtIrgHn9TMBR/nKggM6KNqh08uGwzCNvDQcwoPeQ5hbSGKzY3ghMv7jhdgg5VAYl5OO/mfsBquGWIDaaMYUSGNdF5JyAPGa6qKwalfO6lqNECerN+YD3ZiND0dHhS4NfFRa9DYwX0bWJdzER8zeYXEHuDco9xeUcskC9X+psymcXsVD2IF7cdnGd3eeie9uIF9RwQXs4FQGXAhFHRvUxwGihGNJsFIyCFYX97vPBDvlA2iMIhYIghitgCM+l7PAmfPQSjVhx2nCboMmkFaaQFarCbB9RrGDFaw/VMbh6gWDVUhjfDPBAB8HgmY/2A4Ah1NmuSGBT6QKBEOYqwAhwR9YTd48k4jgvqMG9FitTi/ePhN0qM+E81w4RrXE51pVeONU4e2CKgxaaMJg3U4JS6IaordCE8MWFtQ+1bEg8FUAjrj6WK6zcZCWkOcAEHOUmFOXJWWwQMreclLq/r93nf/PeNss5IJZzM2l6y53R51h7ivCQCqrjzuKEaZ8FCBhDgr24zY9JXzI38VtXPxqUMlVoO63AXV/jUClWPmScMYVwUgKQqoTMWGmfiK5kOYkQVHAJ6gSdTtUbZVjDtHXDs89uBCjI/Ow/vi6HFebik9hA2tzP0xmXE0J+wIxppgUWHGiGLuLgGC0KCF4Ke6X5wbifHVDNrKCW+hEmPdmIJ80Jkl28qc+SvSphdn1zhQ/WnDypsbJq0VOvrXi5NsiJ5xK8DUVYElFwCaVpocnZUPiKuF4ArS8qtGyv0jL91a0fF/bUNmQgStpsPUnZb9GymKp5MdFK1Iuro0V9VisYFFttutPyp4jZd+RstMgYNclq/MSVqWrNWIUxVgJSgUOiPnp4d6S1bvF0mQ7b85X14q3nRpvi9nEj+8tefvexBvFiCEBRxsaSEI5XVPeqnBrrkuuFW1va7QtloZ+XLSk7eLJhhshljX6BFjbrbG213Dybsna1xsEm1hL1nBQ5fLBY9O2LGk8uGXSuHalKOJLhQQWQiCFsAwgWgz8yBeYKYK4JBhLEbSt+l9bpTpwHl/9ejVXvaYtKlXGeqW1qmZf766qkDXzc1dVtSLN+c4Nfu7CwIciSgaIECExm8bMw5e4BhM+6QKf79pUY97drsR7L8UYiX3GAkwlg8jAvCpwEZ9yxkA+OSGQo3F11wJX04ZQhce7q/PL64Jk4fRFV5hjtoyRlSSgzaw92jb+h3XbOmtN3n/YxvsPb+f9mLi3juz1XneWG+8r0scKvCqQlCiOySTzQT5DEmGqCPgcxJUU7C4by5IqQBU6h00n4Hahc9EUOnOVgDufpe4lduSTSVsOa6Q1HoDbkfb1er2bJAZrRhqhT6Y4vVdj7aCpttOOtW9PNtQ2xPKXlx4tb+lmWaLDdIpOOA/wjHw/9AtfXLlsQzbXMScnsnBkObRtbwBA7/xEx6X29nQegu0v/c/kV6/oDVIdRzDwoB0g3TUEBF9RIbwakbEHqZQ3CnPwE1jvDDZ0KTabs++62nfCq5fiX/wPUEsHCK9Ctb5NBwAARi8AAFBLAQIUABQACAAIAKyt7DyvQrW+TQcAAEYvAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAhwcAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
| + | |
| | | | |
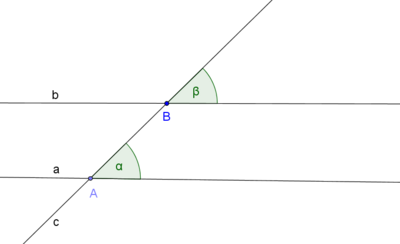
| | == Die Umkehrung des Stufenwinkelsatzes == | | == Die Umkehrung des Stufenwinkelsatzes == |
 und
und  zwei nicht identische Geraden, die durch eine dritte Gerade
zwei nicht identische Geraden, die durch eine dritte Gerade  jeweils geschnitten werden. Es seien ferner
jeweils geschnitten werden. Es seien ferner  und
und  zwei Stufenwinkel, die bei dem Schnitt von
zwei Stufenwinkel, die bei dem Schnitt von 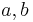 und
und  und die Gerade
und die Gerade  schneiden.
schneiden.