Lösung Aufgabe 11.03 WS 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 11.03) |
(→Lösung User ...) |
||
| Zeile 18: | Zeile 18: | ||
War natürlich ein Fehler, hab's geändert, danke. --[[Benutzer:*m.g.*|*m.g.*]] 19:34, 21. Jan. 2013 (CET)) | War natürlich ein Fehler, hab's geändert, danke. --[[Benutzer:*m.g.*|*m.g.*]] 19:34, 21. Jan. 2013 (CET)) | ||
| − | + | Dürfen wir bei diesem Beweis die euklidische Geometrie anwenden und einfach über die Innenwinkelsumme im Dreieck gehen? | |
=Lösung User ...= | =Lösung User ...= | ||
Version vom 23. Januar 2013, 10:27 Uhr
Aufgabe 11.03Es sei
(Muss es nicht korrekterweise heißen: Beweisen Sie: War natürlich ein Fehler, hab's geändert, danke. --*m.g.* 19:34, 21. Jan. 2013 (CET)) Dürfen wir bei diesem Beweis die euklidische Geometrie anwenden und einfach über die Innenwinkelsumme im Dreieck gehen? Lösung User ... |
 ein Winkel mit den Schenkeln
ein Winkel mit den Schenkeln  und
und  und dem Scheitel
und dem Scheitel  . Ferner sei
. Ferner sei  die Winkelhalbierende von
die Winkelhalbierende von 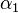 und
und 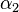 teilt. Auf
teilt. Auf  gegeben.
gegeben. 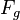 sei der Fußpunkt des Lotes von
sei der Fußpunkt des Lotes von 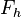 , indem wir auf
, indem wir auf 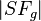 abtragen:
abtragen:

