Winkelmessung: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) |
(→Definition V.4: (Größe eines Winkels)) |
||
| Zeile 14: | Zeile 14: | ||
::Zu jedem Winkel <math>\ \alpha</math> gibt es genau eine reelle Zahl <math>\ \omega</math> zwischen 0 und 180. | ::Zu jedem Winkel <math>\ \alpha</math> gibt es genau eine reelle Zahl <math>\ \omega</math> zwischen 0 und 180. | ||
| − | =====Definition V. | + | =====Definition V.5: (Größe eines Winkels) ===== |
:: Die Zahl <math>\ \omega</math>, die entsprechend des Winkelmaßaxioms einem jeden Winkel <math>\ \alpha</math> eindeutig zugeordnet werden kann, wird die Größe oder das Maß von <math>\ \alpha</math> genannt.<br />In Zeichen: <math>\omega = \left| \alpha \right|</math>. | :: Die Zahl <math>\ \omega</math>, die entsprechend des Winkelmaßaxioms einem jeden Winkel <math>\ \alpha</math> eindeutig zugeordnet werden kann, wird die Größe oder das Maß von <math>\ \alpha</math> genannt.<br />In Zeichen: <math>\omega = \left| \alpha \right|</math>. | ||
Version vom 20. Juni 2010, 12:11 Uhr
Inhaltsverzeichnis |
Winkelmessung
Das Winkelmaß
Was bedeutet es, die Größe eines Winkels zu messen?
| Länge einer Strecke | Größe eines Winkels |
| nichtnegative reelle Zahl | reelle Zahl zwischen 0 und 180 |
Das Winkelmaßaxiom
Axiom IV.1 (Winkelmaßaxiom)
- Zu jedem Winkel
gibt es genau eine reelle Zahl 
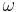zwischen 0 und 180.
- Zu jedem Winkel
Definition V.5: (Größe eines Winkels)
- Die Zahl 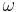, die entsprechend des Winkelmaßaxioms einem jeden Winkel eindeutig zugeordnet werden kann, wird die Größe oder das Maß von genannt.
In Zeichen: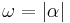
.
- Die Zahl
Winkelkonstruktion
Existenz und Eindeutigkeit des Winkelantragens
Axiom IV.2: (Winkelkonstruktionsaxiom)
- Es sei
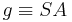eine Gerade in der Ebene 
. Zu jeder reellen Zahl 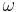mit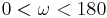 
gibt es in jeder der beiden durch 
bestimmten Halbebenen der Ebene genau einen Strahl 
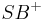mit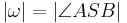 
- Es sei
Winkeladdition
Axiom IV.3: (Winkeladditionsaxiom)
- Wenn der Punkt
zum Inneren des Winkels 
gehört , dann gilt 
.
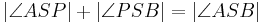- Wenn der Punkt
Satz V.2
- Wenn der Punkt im Inneren des Winkels liegt, dann ist die Größe der beiden Teilwinkel
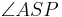und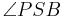 
jeweils kleiner als die Größe des Winkels .
- Wenn der Punkt
Beweis von Satz V.2
Rechte Winkel
Definition V.5 : (Rechter Winkel)
- Wenn ein Winkel die selbe Größe wie einer seiner Nebenwinkel hat, so ist er ein rechter Winkel.
Definition V.6 : (Supplementärwinkel)
- Zwei Winkel, deren Größen zusammen 180 ergeben, sind supplementär.
Axiom IV.4: (Supplementaxiom)
- Nebenwinkel sind supplementär.
Satz V.3 : (Existenz von rechten Winkeln)
- Es gibt rechte Winkel.
Beweis von Satz V.3 :
Wir haben zu zeigen, dass wenigstens ein rechter Winkel existiert.
Nach Definition V.5 ist ein rechter Winkel ein solcher, der das selbe Maß wie einer seiner Nebenwinkel hat.
Das Supplementaxiom (Axiom IV.4) besagt, dass die Summe der Größen zweier Nebenwinkel in jedem Fall 180 beträgt.
Wenn es denn einen rechten Winkel gäbe, so müsste dessen Maß die Hälfte von 180 sein.
Wenn es uns gelänge nachzuweisen, dass es einen Winkel der Größe 90 gibt, so wären wir eigentlich mit unserem Beweis fertig.
In der Tat gibt es einen derartigen Winkel: Das Axiom IV.2 (Winkelkonstruktionsaxiom) besagt, dass es in jeder der beiden Halbebenen einer Ebene bezüglich etwa der Geraden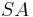 
zu jeder beliebigen Zahl zwischen 0 und 180 genau einen Winkel 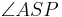gibt, dessen Größe gerade die Zahl zwischen 0 und 180 ist. Die Zahl 90 ist größer als 0 und kleiner als 180 und demzufolge als Winkelmaß zulässig.
Satz V.4 :
- Jeder rechte Winkel hat das Maß 90.
Beweis von Satz V.4 :
- s. Video
