Lösung Aufgabe 11.03 WS 12 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Kommentar --*m.g.* 10:01, 25. Jan. 2013 (CET)) |
*m.g.* (Diskussion | Beiträge) (→Kommentar --*m.g.* 10:01, 25. Jan. 2013 (CET)) |
||
| Zeile 27: | Zeile 27: | ||
==Kommentar --[[Benutzer:*m.g.*|*m.g.*]] 10:01, 25. Jan. 2013 (CET)== | ==Kommentar --[[Benutzer:*m.g.*|*m.g.*]] 10:01, 25. Jan. 2013 (CET)== | ||
*Schritt (2) Begründung: Laut Konstruktion von <math>F_h</math>. Dass wir <math>F_h</math> überhaupt so konstruieren können ist durch Ihre weiteren Begründungen gewährleistet. Solche Begründungen schiebt man besser vor die Beweistabelle. Da ich diese Konstruktion vorgegeben habe, brauchen Sie die Durchführbarkeit nicht zu begründen. (Als Fehler würde ich Ihnen die entsprechende Begründung auf keinen Fall ankreiden.) | *Schritt (2) Begründung: Laut Konstruktion von <math>F_h</math>. Dass wir <math>F_h</math> überhaupt so konstruieren können ist durch Ihre weiteren Begründungen gewährleistet. Solche Begründungen schiebt man besser vor die Beweistabelle. Da ich diese Konstruktion vorgegeben habe, brauchen Sie die Durchführbarkeit nicht zu begründen. (Als Fehler würde ich Ihnen die entsprechende Begründung auf keinen Fall ankreiden.) | ||
| − | *Schritt (6) ist nicht sauber begründet. Sie sollen zeigen: <math>F_h</math> ist der Fußpunkt des Lotes von <math>P</math> auf <math>h</math>. Anders ausgedrückt: Sie sollen zeigen, dass <math>\overline{PF_h}</math> das Lot von <math>P</math> auf <math>h</math> ist. Die Def. Lot bzw. Def. senkrecht geben uns Kriterien an, nach denen wir entscheiden können, ob die Behauptung erfüllt ist. Es bleibt aber vor allem zu zeigen dass die Kriterien erfüllt sind. Sie müssen also begründen, dass <math>PF_h</math> senkrecht auf <math>h</math> steht. | + | *Schritt (6) ist nicht sauber begründet. Sie sollen zeigen: <math>F_h</math> ist der Fußpunkt des Lotes von <math>P</math> auf <math>h</math>. Anders ausgedrückt: Sie sollen zeigen, dass <math>\overline{PF_h}</math> das Lot von <math>P</math> auf <math>h</math> ist. Die Def. Lot bzw. Def. senkrecht geben uns Kriterien an, nach denen wir entscheiden können, ob die Behauptung erfüllt ist. Es bleibt aber vor allem zu zeigen dass die Kriterien erfüllt sind. Sie müssen also begründen, dass <math>PF_h</math> senkrecht auf <math>h</math> steht. Tipp: Weil nach Voraussetzung <math>\overline{PF_g}</math> das Lot von <math>P</math> auf <math>g</math> ist, muss <math>\angle SF_gP</math> ein Rechter sein ... . |
Version vom 25. Januar 2013, 10:19 Uhr
Aufgabe 11.03Es sei
Berichtigung der Erstfassung(Muss es nicht korrekterweise heißen: Beweisen Sie: War natürlich ein Fehler, hab's geändert, danke. --*m.g.* 19:34, 21. Jan. 2013 (CET)) Anfrage Sallie FieldDürfen wir bei diesem Beweis die euklidische Geometrie anwenden und einfach über die Innenwinkelsumme im Dreieck gehen? Lösung User ...
Kommentar --*m.g.* 10:01, 25. Jan. 2013 (CET)
|
 ein Winkel mit den Schenkeln
ein Winkel mit den Schenkeln  und
und  und dem Scheitel
und dem Scheitel  . Ferner sei
. Ferner sei  die Winkelhalbierende von
die Winkelhalbierende von 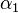 und
und 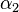 teilt. Auf
teilt. Auf  gegeben.
gegeben. 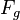 sei der Fußpunkt des Lotes von
sei der Fußpunkt des Lotes von 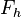 , indem wir auf
, indem wir auf 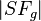 abtragen:
abtragen:

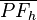 das Lot von
das Lot von 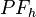 senkrecht auf
senkrecht auf 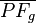 das Lot von
das Lot von 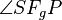 ein Rechter sein ... .
ein Rechter sein ... .

