Lösung von Aufgabe 7.10: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 17: Zeile 17:
  
 
--[[Benutzer:Nicola|Nicola]] 13:52, 6. Jun. 2010 (UTC)
 
--[[Benutzer:Nicola|Nicola]] 13:52, 6. Jun. 2010 (UTC)
 +
 +
 +
noch ein Versuch:<br />Satz III.1: Jede Strecke hat einen und nur einen Mittelpunkt.<br />1. Existenzbeweis bereits in der Vorlesung geführt.<br />2. Eindeutigkeitsbeweis: Jede Strecke hat höchstens einen Mittelpunkt.<br /> Annahme: Es existieren zwei verschiedene Mittelpunkte <math> M_1 </math> und <math> M_2 </math>, die Element von <math> \overline { AB } </math> sind. <br/>
 +
 +
{| class="wikitable "
 +
|+ Beweis
 +
! Nr.
 +
! Beweisschritt
 +
! Begründung
 +
|-
 +
! style="background: #FFDDDD;"|(I)
 +
| <math>\exist M_1 \in \overline { AB }: \left| AM_1 \right| = \left| M_1B \right| </math><br/><math>\exist M_2 \in \overline { AB }: \left| AM_2 \right| = \left| M_2B \right| </math>
 +
| Annahme
 +
|-
 +
! style="background: #FFDDDD;"|(II)
 +
| <math> zw (A, M_1, B)</math><br/><math> zw (A, M_2, B) </math>
 +
| (I), Existenzbeweis, Def. (zw)
 +
|-
 +
! style="background: #FFDDDD;"|(III)
 +
| <math> \left| AM_1 \right| + \left| M_1B \right| = \left| AB \right| </math> <br/> <math> \left| AM_2 \right| + \left| M_2B \right| = \left| AB \right| </math>
 +
| Def (zw), (II)
 +
|-
 +
! style="background: #FFDDDD;"|(IV)
 +
| <math> 2\left| AM_1 \right| = \left| AB \right|</math> <br/> <math> 2\left| AM_2 \right| = \left| AB \right|</math>
 +
| (I), (III), Rechnen in <math> \mathbb{R}  </math>
 +
|-
 +
! style="background: #FFDDDD;"|(V)
 +
| <math> \left| AM_1 \right|= {\left| AB \right| \over 2} </math> <br/> <math> \left| AM_2 \right|= {\left| AB \right| \over 2} </math>
 +
| Rechnen in <math> \mathbb{R}  </math>, (IV)
 +
|-
 +
! style="background: #FFDDDD;"|(VI)
 +
| <math> \left| AM_1 \right|= \left| AM_2 \right|</math>
 +
| (V), Rechnen in <math> \mathbb{R}  </math>
 +
|-
 +
! style="background: #FFDDDD;"|(VII)
 +
| <math> M_1 \equiv M_2 </math><br/> Widerspruch zur Annahme<math> M_1 \not\equiv  M_2 </math><br/> Es existiert höchstens ein Mittelpunkt der Strecke <math> \overline { AB } </math>.
 +
| (VI)
 +
|}
 +
--[[Benutzer:Maude001|Maude001]] 13:16, 20. Jun. 2010 (UTC)

Version vom 20. Juni 2010, 14:16 Uhr

Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt. 


A--M--B

Voraussetzung: koll(A, M, B), zw (A, M, B), 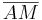\overline{AM} = \overline{MB}

(gemeint ist: \vert AM \vert = \vert MB \vert) --Sternchen 13:25, 10. Jun. 2010 (UTC)

zu zeigen: Es gibt nur einen Punkt M, auf den die o.g. Sachverhalte zutreffen.

M = Mittelpunkt, da Definition III.1: (Mittelpunkt einer Strecke)

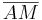\overline{AM} ist eindeutig für \overline{AB} definiert Axiom II.1: (Abstandsaxiom)

--Nicola 13:52, 6. Jun. 2010 (UTC)


noch ein Versuch:
Satz III.1: Jede Strecke hat einen und nur einen Mittelpunkt.
1. Existenzbeweis bereits in der Vorlesung geführt.
2. Eindeutigkeitsbeweis: Jede Strecke hat höchstens einen Mittelpunkt.
Annahme: Es existieren zwei verschiedene Mittelpunkte 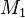M_1 und M_2 , die Element von \overline { AB } sind.

Beweis
Nr. Beweisschritt Begründung
(I) 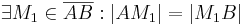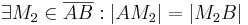\exist M_1 \in \overline { AB }: \left| AM_1 \right| = \left| M_1B \right|
\exist M_2 \in \overline { AB }: \left| AM_2 \right| = \left| M_2B \right| 		Annahme
(II) 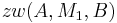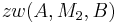zw (A, M_1, B)
zw (A, M_2, B) 		(I), Existenzbeweis, Def. (zw)
(III) 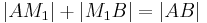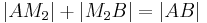\left| AM_1 \right| + \left| M_1B \right| = \left| AB \right|
\left| AM_2 \right| + \left| M_2B \right| = \left| AB \right| 		Def (zw), (II)
(IV) 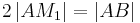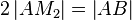2\left| AM_1 \right| = \left| AB \right|
2\left| AM_2 \right| = \left| AB \right| 		(I), (III), Rechnen in \mathbb{R}
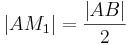(V) \left| AM_1 \right|= {\left| AB \right| \over 2}
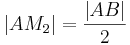
\left| AM_2 \right|= {\left| AB \right| \over 2} 		Rechnen in \mathbb{R} , (IV)
(VI) \left| AM_1 \right|= \left| AM_2 \right| (V), Rechnen in \mathbb{R}
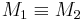(VII) M_1 \equiv M_2
Widerspruch zur Annahme 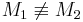M_1 \not\equiv M_2
Es existiert höchstens ein Mittelpunkt der Strecke \overline { AB } . 		(VI)

--Maude001 13:16, 20. Jun. 2010 (UTC)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_7.10&oldid=2072“