Lösung von Aufgabe 12.09 WS 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 12.09) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 12.09) |
||
| Zeile 4: | Zeile 4: | ||
=Aufgabe 12.09= | =Aufgabe 12.09= | ||
| − | Es sei <math>k</math> ein Kreis und <math>\overline{MB}</math> ein Radius von <math>k</math>. <math>t</math> sei eine Gerade mit <math>t \perp MB \wedge B \in t</math>. Beweisen Sie <math>\neg \exist P: P \in t \wedge P \in k \wedge P \not \ | + | Es sei <math>k</math> ein Kreis und <math>\overline{MB}</math> ein Radius von <math>k</math>. <math>t</math> sei eine Gerade mit <math>t \perp MB \wedge B \in t</math>. Beweisen Sie <math>\neg \exist P: P \in t \wedge P \in k \wedge P \not \equi B</math>. |
=Lösung User ...= | =Lösung User ...= | ||
Version vom 27. Januar 2013, 16:48 Uhr
Aufgabe 12.09Es sei Lösung User ...
Lösung User ... |
ein Kreis und 
ein Radius von 
sei eine Gerade mit 
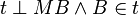. Beweisen Sie Fehler beim Parsen(Unbekannte Funktion „\equi“): \neg \exist P: P \in t \wedge P \in k \wedge P \not \equi B
.
