Lösung von Aufgabe 12.09 WS 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Bemerkung --*m.g.* 16:52, 27. Jan. 2013 (CET)) |
*m.g.* (Diskussion | Beiträge) (→Bemerkung --*m.g.* 16:52, 27. Jan. 2013 (CET)) |
||
| Zeile 14: | Zeile 14: | ||
Der Ansatz, anzunehmen, dass es <math>P</math> doch gibt, liegt nahe. Jetzt sollten Sie aber die Gerade <math>t</math> den Kreis auch zweimal schneiden lassen. Ich hab das Ding zwar <math>t</math> genannt aber nirgends behauptet, es handle sich um die Tangente (die sie natürlich im Endeffekt trotzdem ist). | Der Ansatz, anzunehmen, dass es <math>P</math> doch gibt, liegt nahe. Jetzt sollten Sie aber die Gerade <math>t</math> den Kreis auch zweimal schneiden lassen. Ich hab das Ding zwar <math>t</math> genannt aber nirgends behauptet, es handle sich um die Tangente (die sie natürlich im Endeffekt trotzdem ist). | ||
| − | [[Datei:Senkrecht auf r dann 90.png]] | + | [[Datei:Senkrecht auf r dann 90.png|400px]] |
=Lösung User ...= | =Lösung User ...= | ||
Version vom 27. Januar 2013, 17:15 Uhr
Aufgabe 12.09Es sei Lösung User ...
Bemerkung --*m.g.* 16:52, 27. Jan. 2013 (CET)Ich hatte natürlich zunächst einen Fehler in der Aufgabenformulierung. Aber Sie haben die Aufgabe schon richtig interpretiert. Wir sollen zeigen, dass der Berührpunkt Der Ansatz, anzunehmen, dass es Lösung User ... |
 ein Kreis und
ein Kreis und  ein Radius von
ein Radius von  sei eine Gerade mit
sei eine Gerade mit 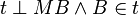 . Beweisen Sie Fehler beim Parsen(Unbekannte Funktion „\equi“): \neg \exist P: P \in t \wedge P \in k \wedge P \not \equi B
.
. Beweisen Sie Fehler beim Parsen(Unbekannte Funktion „\equi“): \neg \exist P: P \in t \wedge P \in k \wedge P \not \equi B
.

 der einzige Punkt ist, den
der einzige Punkt ist, den  doch gibt, liegt nahe. Jetzt sollten Sie aber die Gerade
doch gibt, liegt nahe. Jetzt sollten Sie aber die Gerade 

