Lösung von Aufgabe 12.06 WS 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Bemerkungen --*m.g.* 09:48, 31. Jan. 2013 (CET)) |
*m.g.* (Diskussion | Beiträge) (→Bemerkungen --*m.g.* 09:48, 31. Jan. 2013 (CET)) |
||
| Zeile 26: | Zeile 26: | ||
#Die korrekte Begründung der Parallelen muss also lauten: Existenz der Parallelen. | #Die korrekte Begründung der Parallelen muss also lauten: Existenz der Parallelen. | ||
# Die weitere Lösung ist nicht korrekt. Sie ist aber sehr wertvoll hinsichtlich der Verdeutlichung eines grundlegenden Fehlers, der immer wieder gemacht wird. Man lässt sich von der Figur als Ganzem gefangen nehmen und versäumt wichtige Aspekte der Figuranalyse. Die Psychologen nennen diesen Fehleraspekt: Figurkonzept. Sie haben damit ein grundlegendes Problem, das Schüler mit der Geometrie haben am eigenen Leib erfahren. Diese Erfahrung ist für Ihre spätere Tätigkeit in der Schule wahrscheinlich mehr Wert, als die korrekte Lösung der Aufgabe. | # Die weitere Lösung ist nicht korrekt. Sie ist aber sehr wertvoll hinsichtlich der Verdeutlichung eines grundlegenden Fehlers, der immer wieder gemacht wird. Man lässt sich von der Figur als Ganzem gefangen nehmen und versäumt wichtige Aspekte der Figuranalyse. Die Psychologen nennen diesen Fehleraspekt: Figurkonzept. Sie haben damit ein grundlegendes Problem, das Schüler mit der Geometrie haben am eigenen Leib erfahren. Diese Erfahrung ist für Ihre spätere Tätigkeit in der Schule wahrscheinlich mehr Wert, als die korrekte Lösung der Aufgabe. | ||
| + | #Was hat Sie wohl zu dem Trugschluss gebracht: Sie haben richtig erkannt, dass entsprechend des Wechselwinkelsatzes, die von Ihnen gekennzeichneten Winkel kongruent sind. Sie schauen sich das Gesamtgebilde an: Viele Paare kongruenter Winkel und einige gemeinsame Seiten. Schnellschuss: alle Teildreiecke sind einander kongruent. | ||
| + | #Das Fatale ist: Der Schluss, den Sie vorschnell ziehen, ist sogar wahr. Sie liefern allerdings nicht die korrekte Begründung. | ||
| + | #Der Teufel steckt im Detail. Wir müssten zeigen, dass jedes äußere Teildreieck jeweils zum inneren Teildreieck (dem ursprünglich gegebenen Dreieck) kongruent sind: Nur bei den Paaren (äußeres Dreieck, inneres Dreieck) haben wir gemeinsame Seiten und ohne Seiten werden wir keine Dreieckskongruenz nachweisen können. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
Version vom 31. Januar 2013, 10:11 Uhr
Aufgabe 12.06Beweisen Sie: Die Höhen eines Dreiecks (bzw. die Geraden, die durch die Höhen eindeutig bestimmt sind) schneiden einander in genau einem Punkt.
Lösung User Caro44--Caro44 13:53, 30. Jan. 2013 (CET) Lösung User B.....
Bemerkungen --*m.g.* 09:48, 31. Jan. 2013 (CET)
|
 ein Dreieck. Von diesem Dreieck wissen Sie bereits, dass sich seine Mittelsenkrechten in genau einem Punkt schneiden. Konstruieren aus
ein Dreieck. Von diesem Dreieck wissen Sie bereits, dass sich seine Mittelsenkrechten in genau einem Punkt schneiden. Konstruieren aus 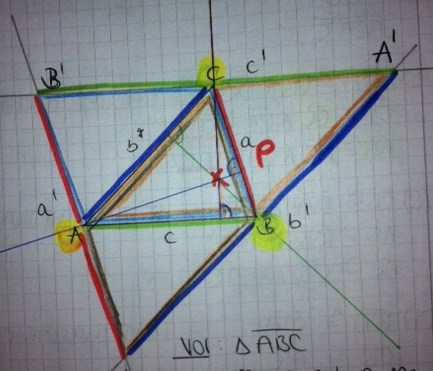


 außerhalb einer Geraden
außerhalb einer Geraden  geht eine zu
geht eine zu  . Was wir nicht beweisen können und deshalb axiomatisch fordern, ist die Tatsache, dass es höchstens eine solche Gerade geben kann.
. Was wir nicht beweisen können und deshalb axiomatisch fordern, ist die Tatsache, dass es höchstens eine solche Gerade geben kann.

