Lösung von Aufgabe 12.08 WS 12 13: Unterschied zwischen den Versionen
Sylvia (Diskussion | Beiträge) (→Lösung User Sylvia) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 15: | Zeile 15: | ||
So, da wir ja leider diesen Mittwoch im Tutorium nicht ganz durchgekommen sind, kommen jetzt die Lösungen. Schaut sie euch bitte durch, falls ihr Fragen dazu habt könnt ihr sie hier oder nächste Woche im Tutorium stellen.<br /><br />--[[Benutzer:Sylvia|Sylvia]] 19:09, 31. Jan. 2013 (CET)<br /> | So, da wir ja leider diesen Mittwoch im Tutorium nicht ganz durchgekommen sind, kommen jetzt die Lösungen. Schaut sie euch bitte durch, falls ihr Fragen dazu habt könnt ihr sie hier oder nächste Woche im Tutorium stellen.<br /><br />--[[Benutzer:Sylvia|Sylvia]] 19:09, 31. Jan. 2013 (CET)<br /> | ||
| − | [[Datei:220130131_183306.jpg]] | + | [[Datei:220130131_183306.jpg| 400px]] |
=Lösung User ...= | =Lösung User ...= | ||
Aktuelle Version vom 3. Februar 2013, 17:52 Uhr
Aufgabe 12.08Sie wissen im Folgenden nicht mehr und nicht weniger über Parallelogramme, als dass diese Vierecke mit zwei Paaren zueinander paralleler Seiten sind und dass die gegenüberliegenden Seiten diese Vierecke kongruent zueinander sind.Rauten sind für Sie Parallelogramme, in denen alle Seiten gleichlang sind. Es sei Beweisen Sie
Lösung SylviaSo, da wir ja leider diesen Mittwoch im Tutorium nicht ganz durchgekommen sind, kommen jetzt die Lösungen. Schaut sie euch bitte durch, falls ihr Fragen dazu habt könnt ihr sie hier oder nächste Woche im Tutorium stellen.
Lösung User ... |
ein Parallelogramm mit 
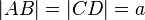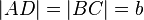und 
und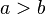 
.
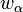die Winkelhalbierende des Winkels 
, 
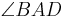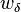sei die Winkelhalbierende des Winkels 
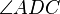. Sie dürfen davon ausgehen, dass 
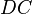im Punkt 
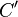schneidet. Analog schneidet 
in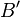 
.
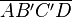ist eine Raute.
