Lösung von Aufgabe 4.1 P (WS 12 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 7: | Zeile 7: | ||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
| − | Im Grunde, sagt die Äquivalenz ja aus, dass sowohl die Implikation und ihre Umkehrung gilt oder?!? --[[Benutzer:Hakunamatata|Hakunamatata]] 17:34, 3. Feb. 2013 (CET) | + | Im Grunde, sagt die Äquivalenz ja aus, dass sowohl die Implikation und ihre Umkehrung gilt oder?!? --[[Benutzer:Hakunamatata|Hakunamatata]] 17:34, 3. Feb. 2013 (CET)<br /> |
| + | |||
| + | Nein, ich glaube nicht. Das ist ja nicht die Umkehrung, sondern die Kontraposition. | ||
| + | Umkehrung wäre <math>\ B \Rightarrow A</math> . Und die sind ja nicht äquivalent zueinander; die Kontraposition und die Implikation aber schon, laut Wahrheitstabelle.--[[Benutzer:TobiWan|TobiWan]] 18:24, 3. Feb. 2013 (CET)<br /> | ||
Version vom 3. Februar 2013, 18:24 Uhr
Beweisen Sie mit Hilfe einer Wahrheitstabelle:
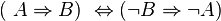
Inwiefern hilft Ihnen diese Äquvalenz, wenn Sie einen geometrischen Satz beweisen wollen?
Im Grunde, sagt die Äquivalenz ja aus, dass sowohl die Implikation und ihre Umkehrung gilt oder?!? --Hakunamatata 17:34, 3. Feb. 2013 (CET)
Nein, ich glaube nicht. Das ist ja nicht die Umkehrung, sondern die Kontraposition.
Umkehrung wäre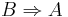 
. Und die sind ja nicht äquivalent zueinander; die Kontraposition und die Implikation aber schon, laut Wahrheitstabelle.--TobiWan 18:24, 3. Feb. 2013 (CET)
