Probeklausur WS 12 13 Aufgabe 4: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe a) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> | ||
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| + | |||
| + | <!--- ------------------------------------------------------------------------------------------ ---> | ||
| + | |||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 61: | Zeile 67: | ||
==Lösung User ...== | ==Lösung User ...== | ||
| + | |||
| + | |||
| + | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
| + | |} | ||
| + | </div> | ||
| + | [[Kategorie:Einführung_S]] | ||
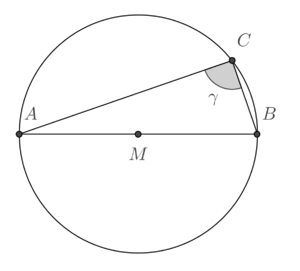
 ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  , auf
, auf  gegeben.
gegeben. 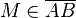 ,
,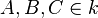 ,
, 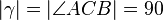 °
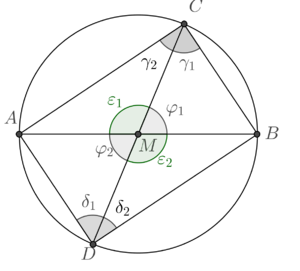
°  eingezeichnet und zum Viereck
eingezeichnet und zum Viereck 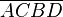 ergänzt. Die Korrektheit dieser Konstruktion muss nicht begründet werden. Ergänzen Sie das folgende Beweisfragment:
ergänzt. Die Korrektheit dieser Konstruktion muss nicht begründet werden. Ergänzen Sie das folgende Beweisfragment:
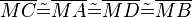
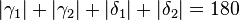 °
° 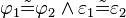
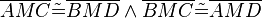
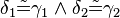
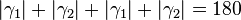 °
° 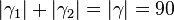 °
° 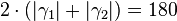 °
° 
