Bresenham-Algorithmus (in Arbeit): Unterschied zwischen den Versionen
(→Darstellungsmöglichkeiten von Geraden) |
(→Hessesche Normalform) |
||
| Zeile 1: | Zeile 1: | ||
=Darstellungsmöglichkeiten von Geraden= | =Darstellungsmöglichkeiten von Geraden= | ||
==Hessesche Normalform== | ==Hessesche Normalform== | ||
| + | |||
| + | Wir kennen schon verschiedene Möglichkeiten Geraden in Form von Gleichungen darzustellen. Die bekanntest dürfte die Steigungsform | ||
| + | y = mx + c | ||
| + | sein. | ||
| + | |||
| + | Durch die Einführung des Skalarproduktes bietet sich eine neue einfachere Beschreibungsform von Geraden an. | ||
| + | |||
| + | Hierfür benötigen wir den Begriff des Normalenvektors. | ||
| + | |||
| + | Definition Normalenvektor: | ||
| + | Sei g eine Gereade mit g : x = s + r * t | ||
| + | |||
| + | Ein Vektor v heißt Normalenvektor zu einer Geraden g im Fußpunkt P genau dann wenn <v,r> = 0 und P = v schnitt r | ||
| + | |||
| + | Es ist offensichtlich, dass es im Raum unendlich vieler solcher Normalenvektoren zu einem gegebenen Punkt und einer Geraden gibt. | ||
=Allgemeines zum Bresenham Algorithmus= | =Allgemeines zum Bresenham Algorithmus= | ||
Version vom 4. Februar 2013, 17:07 Uhr
Inhaltsverzeichnis |
Darstellungsmöglichkeiten von Geraden
Hessesche Normalform
Wir kennen schon verschiedene Möglichkeiten Geraden in Form von Gleichungen darzustellen. Die bekanntest dürfte die Steigungsform y = mx + c sein.
Durch die Einführung des Skalarproduktes bietet sich eine neue einfachere Beschreibungsform von Geraden an.
Hierfür benötigen wir den Begriff des Normalenvektors.
Definition Normalenvektor: Sei g eine Gereade mit g : x = s + r * t
Ein Vektor v heißt Normalenvektor zu einer Geraden g im Fußpunkt P genau dann wenn <v,r> = 0 und P = v schnitt r
Es ist offensichtlich, dass es im Raum unendlich vieler solcher Normalenvektoren zu einem gegebenen Punkt und einer Geraden gibt.
Allgemeines zum Bresenham Algorithmus
Motivation des Algorithmus
Der Bresenham-Algorihtmus, ist ein Verfahren um Graden bzw. Kreise möglichst "gut" auf Anzeigegeräten zu zeichnen. Hier heisst "gut", dass die Abweichung zwischen dem gezeichneten und dem gedachten Objekt möglichst gering ist.
Das Problem beim Darstellen einer Strecke auf einem Anzeigegerät ist, dass das erzeugte Bild nur durch endlich viele Punkte aufgebaut ist. Dadurch entstehen "Lücken" beim zeichnen. Da unser Auge nur eine endliche Auflösung verarbeiten kann, scheint uns ein Bild auf dem Monitor nicht durch einzelne Punkte aufgebaut zu sein, sondern es entstehen für uns geometrische Formen, die wir mit unserer Vorstellung von mathematischen Objekten in Einklang bringen können.
Eine Gerade wie wir sie auf dem Bildschirm wahrnehmen.
Gerade in normaler Größe
Hier sieht man dieselbe Gerade um das 8fache vergrößert.
Gerade bis auf die Pixeleben vergrößert
Effektivität des Algorithmus
Dieser Algorithmus ist auch in heutiger Zeit, in seiner Geschwindigkeit und Einfachheit ungeschlagen, da die Rechenoperationen sich auf Addition und die Multiplikation mit zwei beschränken lässt. Dadurch kann dieser Rechenalgorithmus direkt in die Hardware der Grafikkarten implementiert werden.
Obwohl in den Rechentermen Potenzen auftreten, kann man diese umgehen.
Hierfür betrachten wir den Ausdruck:
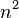
die zweite Binomische Formel liefert:
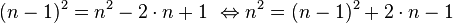
durch rekursives Anwenden dieser Formel lassen sich Potenzen solange vereinfachen bis die Basis Eins erreicht ist und damit die Potenz verschwindet.
Multiplikation mit zwei
Eine Multiplikation mit der Zwei ist für einen Computer eine elementare Rechenoperation, da die sogenannte Shift Operation (Verrückungsoperation) durchgeführt werden kann.
Wir erinnern uns an die Darstellung von Zahlen im Binärsystem.
| Wertigkeit der Stelle | 2^7 = 128 | 2^6 = 64 | 2^5 = 32 | 2^4 = 16 | 2^3 = 8 | 2^2 = 4 | 2^1 = 2 | 2^0 = 1 |
|---|---|---|---|---|---|---|---|---|
| Binärzahl | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
Hier wird die Zahl (im Dezimalsystem) dargestellt
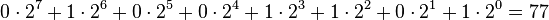
Multiplizerien wir nun mit zwei, so folgt:
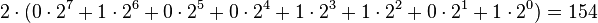

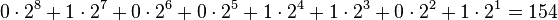
Also die Zahl 154 (Dezimal) in Binärdarstellung:
| Wertigkeit der Stelle | 2^7 = 128 | 2^6 = 64 | 2^5 = 32 | 2^4 = 16 | 2^3 = 8 | 2^2 = 4 | 2^1 = 2 | 2^0 = 1 |
|---|---|---|---|---|---|---|---|---|
| Binärzahl | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
Vergleichen wir nun die Darstellung der Zahl 77 mit der Darstellung der Zahl 154, so fällt auf, dass durch die Multiplikation mit Zwei jedes Bit um eine Stelle nach links verschoben wurde.

