Probeklausur WS 12 13 Aufgabe 3: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Lösung User ...) |
(→Lösung User ...) |
||
| Zeile 20: | Zeile 20: | ||
| − | ==Lösung User ... | + | ==Lösung User Aaliyah== |
| + | |||
| + | Wenn in einem Viereck die gegenüberliegenden Innenwinkel supplementär sind, dann ist das Viereck ein Sehnenviereck.--[[Benutzer:Aaliyah|Aaliyah]] 19:06, 4. Feb. 2013 (CET) | ||
==Lösung User ...== | ==Lösung User ...== | ||
Version vom 4. Februar 2013, 19:06 Uhr
|
Aufgabe aUnter Satz (I) wollen wir den Satz über die gegenüberliegenden Winkel im Sehnenviereck verstehen. Formulieren Sie diesen in der Wenn-Dann-Form. Lösung User AaliyahWenn ein Viereck ein Sehnenviereck ist, dann sind seine gegenüberliegenden Innenwinkel supplementär.--Aaliyah 19:04, 4. Feb. 2013 (CET) Lösung User ...Aufgabe bSatz (II) sei die Umkehrung von Satz (I). Formulieren Sie Satz (II).
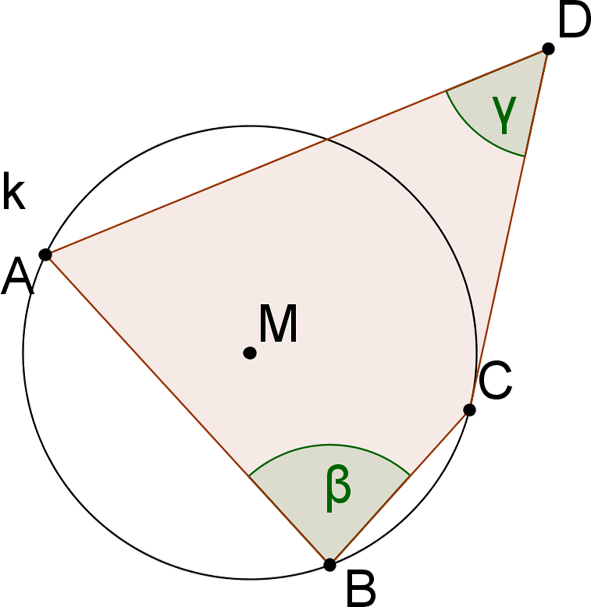
Lösung User AaliyahWenn in einem Viereck die gegenüberliegenden Innenwinkel supplementär sind, dann ist das Viereck ein Sehnenviereck.--Aaliyah 19:06, 4. Feb. 2013 (CET) Lösung User ...Aufgabe cSatz (I) sei bewiesen. Der Beweis von Satz (II) steht aus. Führen Sie den Beweis für eine Konstellation entsprechend der Skizze aus Abb. 01.
Lösung User ...Lösung User ...Aufgabe dAuch Satz (II) lässt sich vollständig beweisen. Formulieren Sie ein Sehnenviereckskriterium.
Lösung User ...Lösung User ... |