Probeklausur WS 12 13 Aufgabe 4: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
(→Lösung User ...) |
||
| Zeile 24: | Zeile 24: | ||
!Nr.!!Beweisschritt!!Begründung | !Nr.!!Beweisschritt!!Begründung | ||
|- | |- | ||
| − | | (I) || <math>\overline{MC} \tilde= \overline{MA} \tilde= \overline{MD} \tilde= \overline{MB}</math> || ... | + | | (I) || <math>\overline{MC} \tilde= \overline{MA} \tilde= \overline{MD} \tilde= \overline{MB}</math> || ...Vor., Definition Abstand eines Punktes von k zu M (Radius eines Kreises) |
|- | |- | ||
| − | | (II) ||<math>|\gamma_1|+|\gamma_2| + |\delta_1| + |\delta_2|=180</math>° || ... | + | | (II) ||<math>|\gamma_1|+|\gamma_2| + |\delta_1| + |\delta_2|=180</math>° || ...Vor., Sehnenviereckskriterium (?) |
|- | |- | ||
| − | | (III) || <math>\varphi_1 \tilde=\varphi_2 \wedge \varepsilon_1 \tilde= \varepsilon_2</math> || ... | + | | (III) || <math>\varphi_1 \tilde=\varphi_2 \wedge \varepsilon_1 \tilde= \varepsilon_2</math> || ... Vor., Def. Scheitelwinkel, (I), SWS |
|- | |- | ||
| − | | (IV) || <math>\overline{AMC} \tilde= \overline{BMD} \wedge \overline{BMC} \tilde=\overline{AMD}</math> || ... | + | | (IV) || <math>\overline{AMC} \tilde= \overline{BMD} \wedge \overline{BMC} \tilde=\overline{AMD}</math> || ... (III), Def. Dreieckskongruenz |
|- | |- | ||
| − | |(V)|| <math>\delta_1 \tilde= \gamma_1 \wedge \delta_2 \tilde= \gamma_2</math> || ... | + | |(V)|| <math>\delta_1 \tilde= \gamma_1 \wedge \delta_2 \tilde= \gamma_2</math> || ... (IV), (II), Rechnen in R |
|- | |- | ||
| − | |(VI)||<math> |\gamma_1|+|\gamma_2| + |\gamma_1| + |\gamma_2|=180</math>° || ... | + | |(VI)||<math> |\gamma_1|+|\gamma_2| + |\gamma_1| + |\gamma_2|=180</math>° || ... (V), Rechnen in R |
|- | |- | ||
|(VIII)|| <math>|\gamma_1|+|\gamma_2| = |\gamma|=90</math>° || ... | |(VIII)|| <math>|\gamma_1|+|\gamma_2| = |\gamma|=90</math>° || ... | ||
|- | |- | ||
| − | |(VII)|| <math>2\cdot\left(|\gamma_1|+|\gamma_2| \right)=180</math>° || ... | + | |(VII)|| <math>2\cdot\left(|\gamma_1|+|\gamma_2| \right)=180</math>° || ... (VI), Rechnen in R |
|} | |} | ||
| + | |||
==Lösung User ...== | ==Lösung User ...== | ||
{| class="wikitable" | {| class="wikitable" | ||
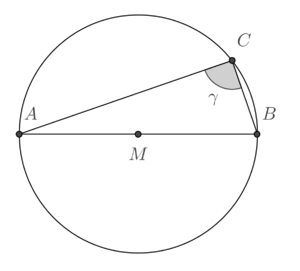
 ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  , auf
, auf  gegeben.
gegeben. 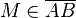 ,
,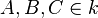 ,
, 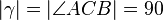 °
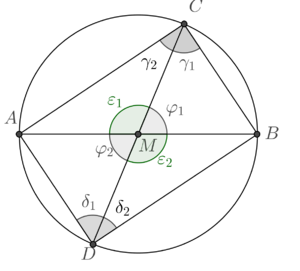
°  eingezeichnet und zum Viereck
eingezeichnet und zum Viereck 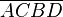 ergänzt. Die Korrektheit dieser Konstruktion muss nicht begründet werden. Ergänzen Sie das folgende Beweisfragment:
ergänzt. Die Korrektheit dieser Konstruktion muss nicht begründet werden. Ergänzen Sie das folgende Beweisfragment:
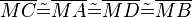
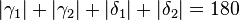 °
° 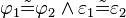
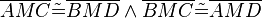
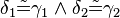
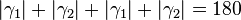 °
° 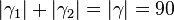 °
° 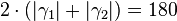 °
° 
