Probeklausur WS 12 13 Aufgabe 4: Unterschied zwischen den Versionen
(→Lösung User ...) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 65: | Zeile 65: | ||
==Lösung User ...lw)...== | ==Lösung User ...lw)...== | ||
| − | Wenn ein alle drei Punkte A,B,C eines Dreiecks auf dessen Umkreis k liegen und die Basis <math>\overline{AB}</math> ein Druchmesser von k ist, dann ist das Dreieck ein rechtwinkliges Dreieck. --[[Benutzer:...lw)...|...lw)...]] 11:06, 5. Feb. 2013 (CET) | + | Wenn ein alle drei Punkte A,B,C eines Dreiecks auf dessen Umkreis k liegen und die Basis <math>\overline{AB}</math> ein Druchmesser von k ist, dann ist das Dreieck ein rechtwinkliges Dreieck. --[[Benutzer:...lw)...|...lw)...]] 11:06, 5. Feb. 2013 (CET)<br /> |
| − | + | geht so leider gar nicht--[[Benutzer:*m.g.*|*m.g.*]] 14:19, 5. Feb. 2013 (CET) | |
==Lösung User ...== | ==Lösung User ...== | ||
Version vom 5. Februar 2013, 14:19 Uhr
|
Aufgabe aEs sei Lösung ...lw)...
Lösung User ...
Aufgabe bFormulieren Sie den unter a) bewiesenen Satz in allgemeinerer Form unter Verwendung der Begriffe Dreieck und Umkreis in der Form Wenn-Dann. Lösung User ...lw)...Wenn ein alle drei Punkte A,B,C eines Dreiecks auf dessen Umkreis k liegen und die Basis Lösung User ... |
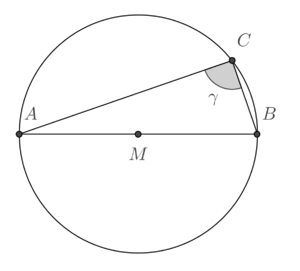
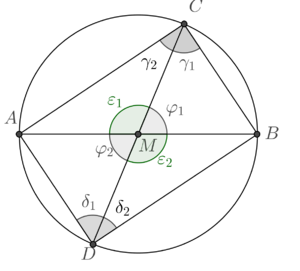
 ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  , auf
, auf  gegeben.
gegeben. 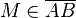 ,
,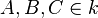 ,
, 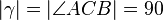 °
°  eingezeichnet und zum Viereck
eingezeichnet und zum Viereck 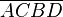 ergänzt. Die Korrektheit dieser Konstruktion muss nicht begründet werden. Ergänzen Sie das folgende Beweisfragment:
ergänzt. Die Korrektheit dieser Konstruktion muss nicht begründet werden. Ergänzen Sie das folgende Beweisfragment:
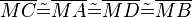
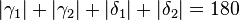 °
° 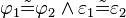
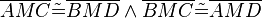
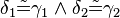
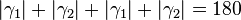 °
° 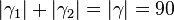 °
° 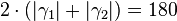 °
°  ein Druchmesser von k ist, dann ist das Dreieck ein rechtwinkliges Dreieck. --
ein Druchmesser von k ist, dann ist das Dreieck ein rechtwinkliges Dreieck. --
