Lösung von Aufg. 6.5P (WS 12/13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 6: | Zeile 6: | ||
Die Kontraposition ist ja :<math>\neg B\Rightarrow \neg A</math> <br /> | Die Kontraposition ist ja :<math>\neg B\Rightarrow \neg A</math> <br /> | ||
Daher: Wenn die Schnittmenge (Durchschnitt) zweier Punktmengen nicht konvex ist, dann ist mindestens eine Punktmenge konkav.--[[Benutzer:Hakunamatata|Hakunamatata]] 19:32, 4. Feb. 2013 (CET)<br /> | Daher: Wenn die Schnittmenge (Durchschnitt) zweier Punktmengen nicht konvex ist, dann ist mindestens eine Punktmenge konkav.--[[Benutzer:Hakunamatata|Hakunamatata]] 19:32, 4. Feb. 2013 (CET)<br /> | ||
| + | *Korrekt.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 16:09, 5. Feb. 2013 (CET) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Aktuelle Version vom 5. Februar 2013, 16:09 Uhr
Formulieren Sie die Kontraposition der Implikation aus Aufgabe 6.4. (Der Durchschnitt zweier konvexer Punktmengen ist konvex. )
Die Teilmengen einer Konkaven Menge sind Konkav. --Würmli 11:54, 4. Feb. 2013 (CET)
- Das ist nicht die Kontraposition. Sorry, ich verstehe auch gar nicht, wie du jetzt auf Teilmenge kommst.--Tutorin Anne 13:42, 4. Feb. 2013 (CET)
Die Kontraposition ist ja :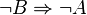
Daher: Wenn die Schnittmenge (Durchschnitt) zweier Punktmengen nicht konvex ist, dann ist mindestens eine Punktmenge konkav.--Hakunamatata 19:32, 4. Feb. 2013 (CET)
- Korrekt.--Tutorin Anne 16:09, 5. Feb. 2013 (CET)

