Lösung von Aufgabe 10.5P (WS 12 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 27: Zeile 27:
 
<br />
 
<br />
 
* Ich habe schon mal eine mögliche Beweisführung angegeben. Viel Spaß beim Nachvollziehen und begründen. (Vergesst nicht, euch eine Skizze zu machen, dann fällt das Begründen einfacher)--[[Benutzer:Tutorin Anne|Tutorin Anne]] 17:48, 28. Jan. 2013 (CET)<br />
 
* Ich habe schon mal eine mögliche Beweisführung angegeben. Viel Spaß beim Nachvollziehen und begründen. (Vergesst nicht, euch eine Skizze zu machen, dann fällt das Begründen einfacher)--[[Benutzer:Tutorin Anne|Tutorin Anne]] 17:48, 28. Jan. 2013 (CET)<br />
 +
 +
Hallo Anne, liegt hier in deinem 1. Schritt nicht ein Fehler vor?!? Wir haben bei der Punktspiegelung ja unser Achsenkreuz a verkettet mit b. Wie können wir denn dann im ersten Schritt so drehen, dass a zu b parallel ist?!? müssten wir nicht schreiben, dass a parallel zu g ist?!? --[[Benutzer:Hakunamatata|Hakunamatata]] 18:00, 6. Feb. 2013 (CET)<br />
 +
  
  

Version vom 6. Februar 2013, 18:00 Uhr

Beweisen Sie Satz IX.4: Bei einer Punktspiegelung werden Geraden stets auf parallele Bildgeraden abgebildet.

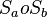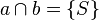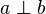Voraussetzung Punktspiegelung S_a o S_b mit a \cap b = \{S\} und a \perp b)
Behauptung 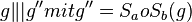g \|| g'' mit g'' = S_a o S_b (g)


Nr. Beweisschritt Begründung
1 Wir drehenn a und b bei festem S so, dass 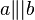a \|| b (Begründung 1)
2 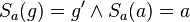S_a(g) = g' \wedge S_a(a)=a (Begründung 2)
3 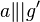a \|| g' (Begründung)
4 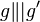g \|| g' (Begründung)
5 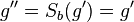g'' = S_b (g') = g' (Begründung)
6 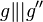g \|| g'' (Begründung)


  • Ich habe schon mal eine mögliche Beweisführung angegeben. Viel Spaß beim Nachvollziehen und begründen. (Vergesst nicht, euch eine Skizze zu machen, dann fällt das Begründen einfacher)--Tutorin Anne 17:48, 28. Jan. 2013 (CET)

Hallo Anne, liegt hier in deinem 1. Schritt nicht ein Fehler vor?!? Wir haben bei der Punktspiegelung ja unser Achsenkreuz a verkettet mit b. Wie können wir denn dann im ersten Schritt so drehen, dass a zu b parallel ist?!? müssten wir nicht schreiben, dass a parallel zu g ist?!? --Hakunamatata 18:00, 6. Feb. 2013 (CET)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_10.5P_(WS_12_13)&oldid=21620“