Geraden 2012 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Abstand eines Punktes zu einer Geraden)
(→‎Abstand eines Punktes zu einer Geraden)
Zeile 108: Zeile 108:
 
Sei eine Gerade g in Hesseform mit <math> \vec{n_n} \cdot ( \vec{r} - \vec{a}) = 0 </math> gegeben, dann gilt für den Abstand h des Punktes P von der Geraden g: <br><br>
 
Sei eine Gerade g in Hesseform mit <math> \vec{n_n} \cdot ( \vec{r} - \vec{a}) = 0 </math> gegeben, dann gilt für den Abstand h des Punktes P von der Geraden g: <br><br>
 
<math> |h| = |\vec{n_n} \cdot (\vec{p} - \vec{a})|</math><br><br>
 
<math> |h| = |\vec{n_n} \cdot (\vec{p} - \vec{a})|</math><br><br>
 +
Anmerkung<br>
 
Hierbei ist zu beachten, dass das Vorzeichen des Abstands <math> h </math> von der Lage des Punktes abhängt, da der Normalenvektor mit positiven Vorzeichen die Richtung vom Ursprung zur Geraden hat.<br>
 
Hierbei ist zu beachten, dass das Vorzeichen des Abstands <math> h </math> von der Lage des Punktes abhängt, da der Normalenvektor mit positiven Vorzeichen die Richtung vom Ursprung zur Geraden hat.<br>
 
Also gilt für den Abstand eines Punktes der zwischen Geraden und Nullpunkt liegt, dass dieser negativ ist. Analog  besitzt ein Punkt,der nicht zwischen Geraden und Ursprung liegt, einen positiven Abstand.
 
Also gilt für den Abstand eines Punktes der zwischen Geraden und Nullpunkt liegt, dass dieser negativ ist. Analog  besitzt ein Punkt,der nicht zwischen Geraden und Ursprung liegt, einen positiven Abstand.

Version vom 7. März 2013, 14:10 Uhr

Inhaltsverzeichnis

Darstellung von Geraden

Die Parameterform

Eine Möglichkeit ist es Geraden mit Hilfe von zwei Vektoren darzustellen. Hierfür wir zum einen ein Stützvektor, zum anderen ein Richtungsvektor benötigt.

Normierung eines Vektors

Manchmal ist es bei einem Vektor von größerem Interesse in welche Richtung er zeigt, als welche Länge (Betrag) er besitzt. In solchen Fällen wird der Vektor durch seine Länge geteilt und hat dann damit die Länge Eins. Nun ist es wesentlich bequemer mit diesem normierten Vektor zu rechnen, als mit dem unnormierten Vektor. Rechnerisch ergibt sich der Betrag eines Vektors aus der Wurzel des Skalarproduktes mit sich selbst.

Beispiel:

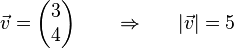
\vec{v} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} \ \ \ \ \ \ \Rightarrow \ \ \ \ \ |\vec{v} | = 5

Nun wird der Vektor durch seinen Betrag geteilt:
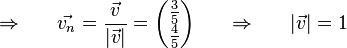
\Rightarrow \ \ \ \ \ \vec{v_n} = \frac{\vec{v}}{|\vec{v}|} = \begin{pmatrix} \frac{3}{5}\\ \frac{4}{5} \end{pmatrix} \ \ \ \ \ \Rightarrow \ \ \ \ \ |\vec{v}| = 1

Der Normalenvektor

Definition des Normalenvektors

Sei g eine Gerade. Ein Vektor 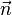\ \vec{n} \ heisst genau dann Normalenvektor von g, wenn 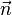\ \vec{n}\ senkrecht zu der Geraden g steht.

Der Punkt A an dem sich ein Normalenvektor mit der Geraden schneidet, wird auch Aufpunkt genannt.



Skizze eines Normalenvektors

Eigenschaften des Normalenvektors

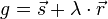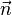Sei g eine Gerade mit \ \ g = \vec{s} + \lambda \cdot \vec{r} \ und \vec{n} der Normalenvektor auf g , mit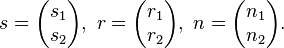 s =\begin{pmatrix} s_1 \\ s_2 \end{pmatrix}, \ r =\begin{pmatrix} r_1 \\ r_2 \end{pmatrix},\ n =\begin{pmatrix} n_1 \\ n_2 \end{pmatrix}.

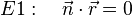
E1:\ \ \ \vec{n} \cdot \vec{r} = 0

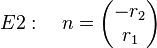
E2:\ \ \ n =\begin{pmatrix} -r_2 \\ r_1 \end{pmatrix}

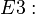E3: Im Raum gibt es unendlich viele Normalenvektoren zu einer Gerade g und einem Aufpunkt A.


Ist in der Ebene von einer Geraden ein Punkt P und ihr Normalenvektor bekannt, so wird diese hierdurch eindeutig beschrieben. Sei 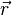\vec{r} ein beliebiger Ortsvektor auf der Geraden g, da der Normalenvektor 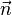\vec{n} senkrecht zu der Geraden 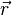\vec{r} steht, so steht 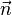\vec{n} auch senkrecht zu jedem anderen Vektor 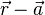\vec{r}- \vec{a} der Geraden g.






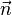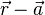Da die beiden Vektoren \vec{n} und \vec{r}-\vec{a} senkrecht zueinander stehen, muss das Skalarprodukt dieser beiden Vektoren Null ergeben:

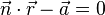
\vec{n} \cdot \vec{r}-\vec{a} = 0

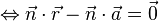
\Leftrightarrow \vec{n} \cdot \vec{r} - \vec{n} \cdot \vec{a} = \vec{0}

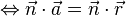
\Leftrightarrow \vec{n} \cdot \vec{a} = \vec{n} \cdot \vec{r}

Hesseform

Herleitung der Hesseform

(Otto Hesse, deutscher Mathematiker, von 1811-1874)

Aus den Eigenschaften des Normalenvektors einer Gerade, wollen wir nun auf eine neue Darstellungsform von Geraden in der Ebene schliessen.

Wir fassen zusammen: Eine Gerade g in der Ebene ist durch einen Punkt A auf der Geraden und einen Normalenvektor n eindeutig festgelegt. Ein jeder Ortsvektor 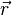\vec{r} eines Punktes der Geraden erfüllt die folgende Gleichung:

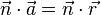
\vec{n} \cdot \vec{a} = \vec{n} \cdot \vec{r}

diese Gleichung wird auch Punktnormalengleichung der Geraden genannt.

Das Skalarprodukt 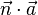\vec{n} \cdot \vec{a} \ ist natürlich bestimmbar, wenn zumindest der Punkt A und ein Normalenvektor 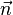\vec{n} \ gegeben sind. Dies ist eine reele Zahl c, also lässt sich die Punktenormalengleichung noch etwas umschreiben:

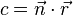
c = \vec{n} \cdot \vec{r}

Diese Gleichung wird nun allgemeine Normalengleichung der Geraden genannt.
Wird nun noch zusätzlich der Normalenvektor 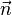\vec{n} normiert so sprechen wir von der Hesseform der Geraden:

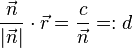
\frac{\vec{n}}{|\vec{n}|} \cdot \vec{r} = \frac{c}{\vec{n}} =: d

Abstand eines Punktes zu einer Geraden

Sei nun eine Gerade 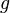\ g \ in Hesseform gegeben:
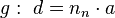
g: \ d = n_n \cdot a
Wobei 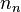\ n_n \ der normierte Normalenvektor und 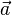\ \vec{a} \ der Ortsvektor eines beliebigen Punktes der Geraden ist.
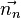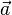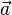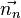Nun betrachten wir den Abstand der Geraden zum Ursprung. Da das Skalarprodukt der Vektoren \vec{n_n} und \vec{a} \ die Länge der senkrechten Projektion von \vec{a} auf \vec{n_n}\ ist, entspricht dieser Abstand genau d .
Betrachten wir nun einen Punkt P der nicht auf der Geraden liegt:


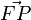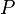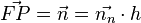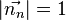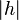Sei nun der Vektor \vec{FP} der Normalenvektor vom Fußpunkt F zum Punkt P\ dann gilt: \vec{FP} = \vec{n} = \vec{n_n} \cdot h , wobei h ein geeignete reele Zahlt ist. Man erkennt nun, da der Betrag von |\vec{n_n}| = 1 , dass |h| der Abstand des Punktes P zur Geraden g sein muss. Da der Punkt F auf der Geraden g liegt muss für ihn die Punktenormalengleichung erfüllt sein:
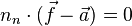
n_n \cdot ( \vec{f} - \vec{a}) = 0




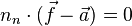Aus n_n \cdot ( \vec{f} - \vec{a}) = 0 folgt wegen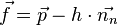 \vec{f} = \vec{p}- h \cdot \vec{n_n}

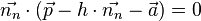
\vec{n_n} \cdot ( \vec{p} - h \cdot \vec{n_n} - \vec{a} ) = 0

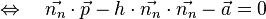
\Leftrightarrow \ \ \ \vec{n_n} \cdot \vec{p} - h \cdot \vec{n_n} \cdot \vec{n_n} - \vec{a} = 0

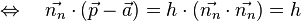
\Leftrightarrow \ \ \ \vec{n_n} \cdot ( \vec{p} - \vec{a}) = h \cdot (\vec{n_n} \cdot \vec{n_n}) = h


Fassen wir zusammen:

Sei eine Gerade g in Hesseform mit 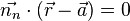\vec{n_n} \cdot ( \vec{r} - \vec{a}) = 0 gegeben, dann gilt für den Abstand h des Punktes P von der Geraden g:

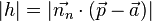
|h| = |\vec{n_n} \cdot (\vec{p} - \vec{a})|

Anmerkung
Hierbei ist zu beachten, dass das Vorzeichen des Abstands h von der Lage des Punktes abhängt, da der Normalenvektor mit positiven Vorzeichen die Richtung vom Ursprung zur Geraden hat.
Also gilt für den Abstand eines Punktes der zwischen Geraden und Nullpunkt liegt, dass dieser negativ ist. Analog besitzt ein Punkt,der nicht zwischen Geraden und Ursprung liegt, einen positiven Abstand.

Von „http://geometrie.zum.de/index.php?title=Geraden_2012_13&oldid=22061“