Übungen 02: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „=Aufgabe 1= Es seien <math>P_1(x_1|y_1)</math> und <math>P_2(x_2|y_2)</math> zwei beliebige voneinander verschiedene Punkte einer Geraden mit der Gleichung <math…“) |
(→Aufgabe 1) |
||
| Zeile 5: | Zeile 5: | ||
<math>\frac{y_2-y_1}{x_2-x_1}=-\frac{a}{b}=m</math> | <math>\frac{y_2-y_1}{x_2-x_1}=-\frac{a}{b}=m</math> | ||
| + | |||
| + | =Aufgabe 2= | ||
| + | |||
| + | Stellen Sie Gleichungen in der Form ax+by=c und der y=mx+b der Geraden durch die gegebenen Punkte auf <br /> | ||
| + | a) <math>P_1(3;-2)</math> und <math>P_2(11;-11)</math><br /> | ||
| + | b)<math>Q_1(\frac{2}{3};\frac{3}{4})</math> und <math>Q_2(8;9) </math> | ||
Version vom 23. April 2013, 09:41 Uhr
Aufgabe 1
Es seien 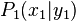 und
und 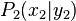 zwei beliebige voneinander verschiedene Punkte einer Geraden mit der Gleichung
zwei beliebige voneinander verschiedene Punkte einer Geraden mit der Gleichung
 (a,b,c
(a,b,c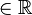 ,
, 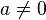 oder
oder 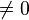 ).
).
Zeigen Sie, das gilt:
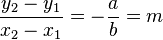
Aufgabe 2
Stellen Sie Gleichungen in der Form ax+by=c und der y=mx+b der Geraden durch die gegebenen Punkte auf
a) 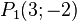 und
und 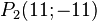
b)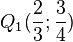 und
und