Lösung von Aufgabe 2.10 SoSe 2013 S: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2.10 SoSe 2013) |
||
| Zeile 4: | Zeile 4: | ||
<!--- ---> | <!--- ---> | ||
=Aufgabe 2.10 SoSe 2013= | =Aufgabe 2.10 SoSe 2013= | ||
| − | Ein Drehellipsoid erhält man wenn man eine Ellipse um die Gerade, die durch ihre beiden Brennpunkte <math>F_1</math> und <math>F_2</math> eindeutig bestimmt ist, rotieren lässt. | + | Ein Drehellipsoid erhält man, wenn man eine Ellipse um die Gerade, die durch ihre beiden Brennpunkte <math>F_1</math> und <math>F_2</math> eindeutig bestimmt ist, rotieren lässt. |
Ergänzen Sie:<br /> | Ergänzen Sie:<br /> | ||
{{Definition|1=Drehellipsoid: <br /> Es seien <math>F_1</math> und <math>F_2</math> zwei Punkte. Ferner sei a eine positive reelle Zahl. Unter einem Drehellipsoid versteht man die Menge aller Punkte <math>P</math>, mit ...}} | {{Definition|1=Drehellipsoid: <br /> Es seien <math>F_1</math> und <math>F_2</math> zwei Punkte. Ferner sei a eine positive reelle Zahl. Unter einem Drehellipsoid versteht man die Menge aller Punkte <math>P</math>, mit ...}} | ||
Aktuelle Version vom 27. April 2013, 13:19 Uhr
Aufgabe 2.10 SoSe 2013Ein Drehellipsoid erhält man, wenn man eine Ellipse um die Gerade, die durch ihre beiden Brennpunkte Definition Drehellipsoid: Lösung von User ...Lösung von User ...Lösung von User ... |
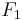 und
und 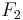 eindeutig bestimmt ist, rotieren lässt.
Ergänzen Sie:
eindeutig bestimmt ist, rotieren lässt.
Ergänzen Sie: , mit ...
, mit ...

