Lösung von Aufgabe 2.01 SoSe 2013 S: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2.01 SoSe 2013) |
||
| Zeile 6: | Zeile 6: | ||
Ergänzen Sie die Lücken durch Verwendung von | Ergänzen Sie die Lücken durch Verwendung von | ||
* ''notwendig aber nicht hinreichend'' | * ''notwendig aber nicht hinreichend'' | ||
| − | *'' hinreichend aber nicht notwendig'' | + | * ''hinreichend aber nicht notwendig'' |
* ''hinreichend'' | * ''hinreichend'' | ||
* ''notwenig'' | * ''notwenig'' | ||
* ''notwendig und hinreichend''. | * ''notwendig und hinreichend''. | ||
| + | * ''weder notwendig noch hinreichend'' | ||
Sollten mehrere diesbezügliche Auswahlmöglichkeiten bestehen, verwenden Sie die schärfste der möglichen Formulierungen. | Sollten mehrere diesbezügliche Auswahlmöglichkeiten bestehen, verwenden Sie die schärfste der möglichen Formulierungen. | ||
# Dafür, dass <math>t</math> die Summe <math>a+b</math> teilt, ist es ... , dass <math>t</math> sowohl <math>a</math> als auch<math> b</math> teilt. (<math>t, a, b \in \mathbb{N}</math>) | # Dafür, dass <math>t</math> die Summe <math>a+b</math> teilt, ist es ... , dass <math>t</math> sowohl <math>a</math> als auch<math> b</math> teilt. (<math>t, a, b \in \mathbb{N}</math>) | ||
| Zeile 18: | Zeile 19: | ||
# Dafür dass ein Viereck ein Rechteck ist, ist es ... , dass alle seine Seiten gleichlang sind. | # Dafür dass ein Viereck ein Rechteck ist, ist es ... , dass alle seine Seiten gleichlang sind. | ||
# Dafür dass ein Viereck ein Rechteck ist, ist es ... , dass es einen rechten Innenwinkel hat und alle seine Seiten gleichlang sind. | # Dafür dass ein Viereck ein Rechteck ist, ist es ... , dass es einen rechten Innenwinkel hat und alle seine Seiten gleichlang sind. | ||
| + | |||
=Lösung von User ...= | =Lösung von User ...= | ||
Aktuelle Version vom 1. Mai 2013, 11:55 Uhr
Aufgabe 2.01 SoSe 2013Ergänzen Sie die Lücken durch Verwendung von
Sollten mehrere diesbezügliche Auswahlmöglichkeiten bestehen, verwenden Sie die schärfste der möglichen Formulierungen.
Lösung von User ...Lösung von User ...Lösung von User ... |
 die Summe
die Summe 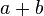 teilt, ist es ... , dass
teilt, ist es ... , dass  als auch
als auch teilt. (
teilt. (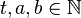 )
)
 ein Rechteck ist, ist es ... , dass
ein Rechteck ist, ist es ... , dass 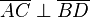 gilt.
gilt.
 rechtwinklig ist, ist es ... , dass kein Innenwinkel von
rechtwinklig ist, ist es ... , dass kein Innenwinkel von 
