Drehungen (2012 13): Unterschied zwischen den Versionen
Gubbel (Diskussion | Beiträge) (→Sätze zu Drehungen) |
Gubbel (Diskussion | Beiträge) (→Sätze zu Drehungen) |
||
| Zeile 33: | Zeile 33: | ||
<br /> | <br /> | ||
| − | Der Punkt C1 wurde an DZ gespiegelt. => Die roten Winkel sind kongruent. Nun spiegelt man an D'Z, wobei <math> \angle </math> DZD' = 1/2 <math> \alpha </math> => Die blauen Winkel sind kongruent. Diese Überlegung kann analog für B und A durchgeführt werden. Die beliebige Drehung ist somit die NAF von zwei Geradenspiegelungen mit dem Schnittwinkel <math> \beta </math> <br /> | + | Der Punkt C1 wurde an DZ gespiegelt. => Die roten Winkel sind kongruent. Nun spiegelt man an D'Z, wobei <math> \angle </math> DZD' = 1/2 <math> \alpha </math> => Die blauen Winkel sind kongruent. Diese Überlegung kann analog für B und A durchgeführt werden. Die beliebige Drehung ist somit die NAF von zwei Geradenspiegelungen mit dem Schnittwinkel <math> \beta </math> <br /> --[[Benutzer:Gubbel|Gubbel]] 20:54, 5. Mai 2013 (CEST)<br /> |
<br /> | <br /> | ||
'''Satz 6.3'''<br /> | '''Satz 6.3'''<br /> | ||
Aktuelle Version vom 5. Mai 2013, 19:54 Uhr
Inhaltsverzeichnis |
Definitionsmöglichkeiten
Definition 1
Unter einer Drehung 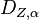 um den Punkt Z mit dem Drehwinkel
um den Punkt Z mit dem Drehwinkel  versteht man eine Abbildung
versteht man eine Abbildung  der Ebene
der Ebene  auf sich, für die gilt:
auf sich, für die gilt:
1. Z ist Fixpunkt bezüglich 
2. 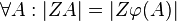 mit
mit 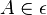 und
und 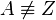
3. 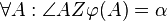 mit
mit 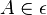 und
und 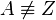
Die Definition entstand aus Vorüberlegungen.
Definition 2
Unter der Drehung 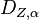 um den Punkt Z mit dem Drehwinkel
um den Punkt Z mit dem Drehwinkel  versteht man die NAF zweier Geradenspiegelungen
versteht man die NAF zweier Geradenspiegelungen 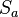 und
und 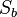 mit
mit 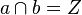 und
und 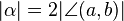
Dieser Definition liegt ein Kriterium zugrunde:
Kriterium D1: Eine Bewegung ist genau dann eine Drehung 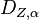 , wenn die die NAF zweier Geradenspiegelungen
, wenn die die NAF zweier Geradenspiegelungen 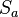 und
und 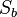 mit
mit 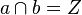 und
und 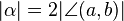 ist.
ist.
Definition 3
Unter einer Drehung vertseht man eine Bewegung mit genau einem Fixpunkt.
Auch diese Definition basiert letztlich auf einem Kriterium (Zur Zeit bleibt noch zu beweisen: Eine Drehung ist die einzige Bewegung mit genau einem Fixpunkt.):
Kriterium D2: Eine Bewegung ist genau dann eine Drehung verschieden von der Identität, wenn sie genau einen Fixpunkt besitzt.
--Jessy* 13:48, 12. Dez. 2012 (CET)
Konstruktion des Bildes eines Punktes bei einer Drehung 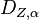
Es seien P und Z zwei verschiedene Punkte der Ebene  und
und 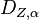 eine Drehung der Ebene
eine Drehung der Ebene  mit dem Drehzentrum Z und dem Drehwinkel
mit dem Drehzentrum Z und dem Drehwinkel  .
.
Drehungen als Bewegungen
Satz 6.1
Jede Drehung ist eine Bewegung.
Sätze zu Drehungen
Satz 6.2
Jede Drehung um das Drehzentrum Z mit dem Drehwinkel  ist die NAF zweier Geradenspiegelungen
ist die NAF zweier Geradenspiegelungen 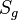 und
und 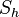 , deren Spiegelachsen nur das Drehzentrum Z gemeinsam haben und für deren Schnittwinkel
, deren Spiegelachsen nur das Drehzentrum Z gemeinsam haben und für deren Schnittwinkel  gilt:
gilt: 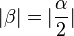
Der Beweis müsste wie folgt laufen...
Der Punkt C1 wurde an DZ gespiegelt. => Die roten Winkel sind kongruent. Nun spiegelt man an D'Z, wobei 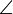 DZD' = 1/2
DZD' = 1/2  => Die blauen Winkel sind kongruent. Diese Überlegung kann analog für B und A durchgeführt werden. Die beliebige Drehung ist somit die NAF von zwei Geradenspiegelungen mit dem Schnittwinkel
=> Die blauen Winkel sind kongruent. Diese Überlegung kann analog für B und A durchgeführt werden. Die beliebige Drehung ist somit die NAF von zwei Geradenspiegelungen mit dem Schnittwinkel 
--Gubbel 20:54, 5. Mai 2013 (CEST)
Satz 6.3
Die NAF zweier Geradenspiegelungen 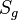 und
und 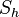 , deren Spiegelachsen genau den Punkt Z gemeinsam haben, ist eine Drehung mit dem Drehzentrum Z und dem Drehwinkel
, deren Spiegelachsen genau den Punkt Z gemeinsam haben, ist eine Drehung mit dem Drehzentrum Z und dem Drehwinkel 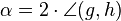
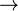 aus den Sätzen 6.2 und 6.3 erhält man das Kriterium D1.
aus den Sätzen 6.2 und 6.3 erhält man das Kriterium D1.
Satz 6.4
Eine Drehung besitzt genau einen Fixpunkt.
Tipp: Beweise den Satz: Die NAF 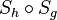 zweier Geradenspiegelungen
zweier Geradenspiegelungen 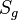 und
und 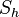 für die gilt: g
für die gilt: g 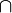 h={Z} besitzt genau einen Fixpunkt.
h={Z} besitzt genau einen Fixpunkt.
Satz 6.5
Jede von der Drehung mit 0°< | | <360° verschiedene Bewegung besitzt mehr oder weniger als genau einen Fixpunkt.
| <360° verschiedene Bewegung besitzt mehr oder weniger als genau einen Fixpunkt.
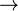 aus den Sätzen 6.4 und 6.5 erhält man das Kriterium D2.
aus den Sätzen 6.4 und 6.5 erhält man das Kriterium D2.

