Beweisen SoSe 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Annahme) |
*m.g.* (Diskussion | Beiträge) (→Beweisbeispiele (direkte Beweise)) |
||
| Zeile 70: | Zeile 70: | ||
==Notwendigkeit des Beweises eines Satzes== | ==Notwendigkeit des Beweises eines Satzes== | ||
::Obige Implikation hinsichtlich der spielerischen Stärke des FC Barcelona in Anhängigkeit der Verfügbarkeit des Weltfußballers Messi wird nur schwer zu beweisen sein und kann damit nicht als Satz im mathematischen Sinne verstanden werden. Mathematische Sätze sind wahre Aussagen und als solche zu beweisen. | ::Obige Implikation hinsichtlich der spielerischen Stärke des FC Barcelona in Anhängigkeit der Verfügbarkeit des Weltfußballers Messi wird nur schwer zu beweisen sein und kann damit nicht als Satz im mathematischen Sinne verstanden werden. Mathematische Sätze sind wahre Aussagen und als solche zu beweisen. | ||
| − | = | + | =Direkte Beweise= |
| + | ==Beispiele für direkte Beweise== | ||
| − | ==Beispiel 1: Der Scheitelwinkelsatz== | + | ===Beispiel 1: Der Scheitelwinkelsatz=== |
| − | ===Vorab=== | + | ====Vorab==== |
Es sei bereits klar, dass Nebenwinkel supplementär sind (sich zu <math>180</math>° ergänzen).<br /> | Es sei bereits klar, dass Nebenwinkel supplementär sind (sich zu <math>180</math>° ergänzen).<br /> | ||
Natürlich seien die Begriffe Scheitelwinkel und Nebenwinkel sauber definiert. | Natürlich seien die Begriffe Scheitelwinkel und Nebenwinkel sauber definiert. | ||
| − | ===Der Satz=== | + | ====Der Satz==== |
:'''Satz: (Scheitelwinkelsatz)''' | :'''Satz: (Scheitelwinkelsatz)''' | ||
::Wenn zwei Winkel <math>\alpha</math> und <math>\beta</math> Scheitelwinkel sind, so haben sie dieselbe Größe. | ::Wenn zwei Winkel <math>\alpha</math> und <math>\beta</math> Scheitelwinkel sind, so haben sie dieselbe Größe. | ||
| − | ===Der Beweis=== | + | ====Der Beweis==== |
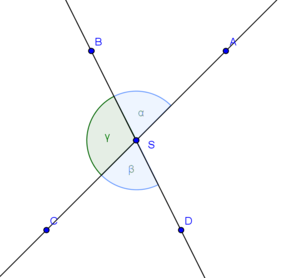
| − | ====Skizze==== | + | =====Skizze===== |
[[File:Beweis Scheitelwinkelsatz.png|300px]] | [[File:Beweis Scheitelwinkelsatz.png|300px]] | ||
====Voraussetzung==== | ====Voraussetzung==== | ||
::<math>\alpha</math> und <math>\beta</math> bilden ein Paar von Scheitelwinkeln | ::<math>\alpha</math> und <math>\beta</math> bilden ein Paar von Scheitelwinkeln | ||
| − | ====Behauptung==== | + | =====Behauptung===== |
::<math>|\alpha| = |\beta|</math> | ::<math>|\alpha| = |\beta|</math> | ||
| − | ====Beweisführung (unter Bezug auf die Beweisskizze)==== | + | =====Beweisführung (unter Bezug auf die Beweisskizze)===== |
# <math>|\alpha| + |\gamma| =180</math>° (Begründung: <math>\alpha</math> und <math>\gamma</math> sind Nebenwinkel und als solche supplementär.) | # <math>|\alpha| + |\gamma| =180</math>° (Begründung: <math>\alpha</math> und <math>\gamma</math> sind Nebenwinkel und als solche supplementär.) | ||
# <math>|\beta| + |\gamma| =180</math>° (Begründung: <math>\beta</math> und <math>\gamma</math> sind Nebenwinkel und als solche supplementär.) | # <math>|\beta| + |\gamma| =180</math>° (Begründung: <math>\beta</math> und <math>\gamma</math> sind Nebenwinkel und als solche supplementär.) | ||
| Zeile 94: | Zeile 95: | ||
q.e.d. | q.e.d. | ||
| − | ==Beispiel 2: Der starke Außenwinkelsatz== | + | ===Beispiel 2: Der starke Außenwinkelsatz=== |
| − | ===Vorab=== | + | ====Vorab==== |
Bereits klar sei: | Bereits klar sei: | ||
# Innenwinkelsumme im Dreieck beträgt <math>180</math>°. | # Innenwinkelsumme im Dreieck beträgt <math>180</math>°. | ||
# Nebenwinkel sind supplementär. | # Nebenwinkel sind supplementär. | ||
# Alle Begriffe sauber definiert. | # Alle Begriffe sauber definiert. | ||
| − | ===Der Satz=== | + | ====Der Satz==== |
:'''Satz: (starker Außenwinkelsatz)''' | :'''Satz: (starker Außenwinkelsatz)''' | ||
::Jeder Außenwinkel eines Dreiecks ist so groß wie die Summe der Größen der beiden Innenwinkel des Dreiecks, die keine Nebenwinkel dieses Außenwinkels sind. | ::Jeder Außenwinkel eines Dreiecks ist so groß wie die Summe der Größen der beiden Innenwinkel des Dreiecks, die keine Nebenwinkel dieses Außenwinkels sind. | ||
| − | ===Skizze=== | + | ====Skizze==== |
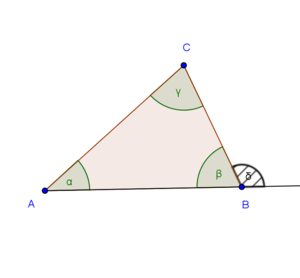
[[File:Beweis Außenwinkelsatz.png|300px]] | [[File:Beweis Außenwinkelsatz.png|300px]] | ||
| − | ===Voraussetzung=== | + | ====Voraussetzung==== |
::Der Winkel <math>\delta</math> sei ein Außenwinkel eines Dreiecks <math>\overline{ABC}</math>. O.B.d.A. sei <math>\delta</math> Nebenwinkel vom Innenwinkel <math>\beta</math> des Dreiecks <math>\overline{ABCD}</math>. (Die beiden Innenwinkel, die zu <math>\delta</math> keine Nebenwinkel sind, seien <math>\alpha</math> und <math>\gamma</math>.) | ::Der Winkel <math>\delta</math> sei ein Außenwinkel eines Dreiecks <math>\overline{ABC}</math>. O.B.d.A. sei <math>\delta</math> Nebenwinkel vom Innenwinkel <math>\beta</math> des Dreiecks <math>\overline{ABCD}</math>. (Die beiden Innenwinkel, die zu <math>\delta</math> keine Nebenwinkel sind, seien <math>\alpha</math> und <math>\gamma</math>.) | ||
| − | ===Behauptung=== | + | ====Behauptung==== |
::<math>|\alpha| + |\gamma| = |\delta|</math> | ::<math>|\alpha| + |\gamma| = |\delta|</math> | ||
| − | ===Beweis=== | + | ====Beweis==== |
Das können Sie selbst. Ergänzen Sie hier den Beweis. Orientieren Sie sich am Beweis des Scheitelwinkelsatzes. | Das können Sie selbst. Ergänzen Sie hier den Beweis. Orientieren Sie sich am Beweis des Scheitelwinkelsatzes. | ||
| − | == | + | ==Was sind direkte Beweise?== |
:: In den obigen Bespielen wurde ausgehend von der Voraussetzung und der Verwendung weiterer bereits bewiesener Sätze die Behauptung unmittelbar hergeleitet. Am Ende der Herleitungskette steht die Behauptung. Man spricht in einem solchen Fall von einem direkten Beweis. | :: In den obigen Bespielen wurde ausgehend von der Voraussetzung und der Verwendung weiterer bereits bewiesener Sätze die Behauptung unmittelbar hergeleitet. Am Ende der Herleitungskette steht die Behauptung. Man spricht in einem solchen Fall von einem direkten Beweis. | ||
Version vom 9. Mai 2013, 16:52 Uhr
ImplikationenBeispieleBeispiel 150px Beispiel 2Wenn ein Trapez ein Rechteck ist, dann sind sein Diagonalen kongruent zueinander. Beispiel 3Wenn ein Boxer während des Kampfes seinem Gegner den Rücken zukehrt, hat er den Kampf verloren. Beispiel 4Wenn zwei Winkel Stufenwinkel an geschnittenen Parallelen sind, dann sind sie kongruent zueinander. Grundlegender Aufbau
Zusammenhang zur hinreichenden BedingungIst die Aussage "Versteckte" ImplikationenBeispieleBeispiel 1: StufenwinkelsatzOhne Wenn-Dann
Wenn-Dann-Form
Voraussetzung
Behauptung
Beispiel 2: Innenwinkelsatz für DreieckeOhne Wenn-Dann
Wenn-Dann-Form
Voraussetzung
Behauptung
Beispiel 3: Umkehrung des ThalessatzesOhne Wenn-Dann
Wenn-Dann-Form
Voraussetzung
Behauptung
Implikationen als mathematische Sätzemathematische Sätze
Implikationen als Sätze
Die Implikation einer Behauptung und die Implikation als Behauptung (umgangssprachlich)
Eine gewagte Behauptung
Notwendigkeit des Beweises eines Satzes
Direkte BeweiseBeispiele für direkte BeweiseBeispiel 1: Der ScheitelwinkelsatzVorabEs sei bereits klar, dass Nebenwinkel supplementär sind (sich zu Der Satz
Der BeweisSkizzeVoraussetzung
BehauptungBeweisführung (unter Bezug auf die Beweisskizze)
q.e.d. Beispiel 2: Der starke AußenwinkelsatzVorabBereits klar sei:
Der Satz
SkizzeVoraussetzung
BehauptungBeweisDas können Sie selbst. Ergänzen Sie hier den Beweis. Orientieren Sie sich am Beweis des Scheitelwinkelsatzes. Was sind direkte Beweise?
Beispiele für WiderspruchsbeweiseWinkel-Seiten-Beziehung im DreieckVorab
Der Satz
VoraussetzungBehauptungAnnahme
Beweisführung
Die Annahme ist somit zu verwerfen. |
 , dann Behauptung
, dann Behauptung  .
.

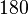 °.
°.
 und
und  Scheitelwinkel sind, so haben sie dieselbe Größe.
Scheitelwinkel sind, so haben sie dieselbe Größe.
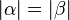
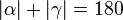 ° (Begründung:
° (Begründung:  sind Nebenwinkel und als solche supplementär.)
sind Nebenwinkel und als solche supplementär.)
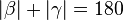 ° (Begründung:
° (Begründung: 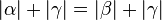 (Begründung: linke Seite von Gleichung 1 ist gleich der linken Seite von Geleichung 2.)
(Begründung: linke Seite von Gleichung 1 ist gleich der linken Seite von Geleichung 2.)
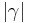 subtrahieren.)
subtrahieren.)
 sei ein Außenwinkel eines Dreiecks
sei ein Außenwinkel eines Dreiecks  . O.B.d.A. sei
. O.B.d.A. sei  . (Die beiden Innenwinkel, die zu
. (Die beiden Innenwinkel, die zu 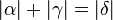
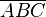 ein Dreieck mit den schulüblichen Bezeichnungen. Wenn der Winkel
ein Dreieck mit den schulüblichen Bezeichnungen. Wenn der Winkel 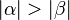
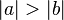
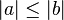 (Das Gegenteil der Behauptung)
(Das Gegenteil der Behauptung)
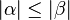 gelten muss.
gelten muss.

