Pfeilklassen: Unterschied zwischen den Versionen
(→Satz) |
(→Pfeilklassen) |
||
| Zeile 5: | Zeile 5: | ||
| − | {{Definition| | + | {{Definition|Zwei Pfeile <math>\vec{AB}</math> und <math>\vec{CD}</math> heißen '''parallelgleich''', wenn gilt: <br /> |
# <math>|AB|=|CD|</math> | # <math>|AB|=|CD|</math> | ||
Version vom 23. Mai 2013, 14:06 Uhr
Pfeilklassen
Definition
Pfeil 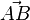
Es seien  und
und  zwei (nicht notwendigerweise) verschiedene Punkte. Der Pfeil
zwei (nicht notwendigerweise) verschiedene Punkte. Der Pfeil 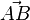 ist das geordnete Paar
ist das geordnete Paar 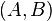 .
.  heißt Anfangspunkt des Pfeils
heißt Anfangspunkt des Pfeils 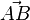 ,
,  heißt Endpunkt des Pfeils
heißt Endpunkt des Pfeils 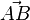 . Jedem Pfeil ist eine Punktmenge zugehörig, Es handelt sich dabei um die Menge der Punkte der Strecke
. Jedem Pfeil ist eine Punktmenge zugehörig, Es handelt sich dabei um die Menge der Punkte der Strecke  . Sollte der Anfangspunkt eines Pfeils mit dem Endpunkt dieses Pfeils zusammenfallen spricht man vom Nullpfeil
. Sollte der Anfangspunkt eines Pfeils mit dem Endpunkt dieses Pfeils zusammenfallen spricht man vom Nullpfeil 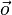 . Zwei Pfeile
. Zwei Pfeile 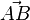 und
und 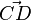 haben einen Punkt gemeinsam falls ihre Punktmengen einen Punkt gemeinsam haben.
haben einen Punkt gemeinsam falls ihre Punktmengen einen Punkt gemeinsam haben.
Definition
Zwei Pfeile 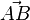 und
und 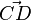 heißen parallelgleich, wenn gilt:
heißen parallelgleich, wenn gilt:
-
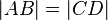
-
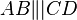
-
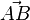 und
und 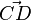 sind gleichorientiert.
sind gleichorientiert.
Satz
Die Relation parallelgleich ist eine Äquivalenzrelation auf der Menge der Pfeile des Raumes bzw. der Ebene.
D.h. 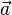 ist parallelgleich(
ist parallelgleich(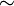 ) zu
) zu 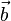 , wenb gilt:
, wenb gilt:
a) Reflexivität: 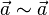
b) Symmetrie: 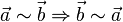
c) Transitivität: 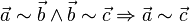
Definition
Eine Pfeilklasse ist eine Äquivalenzklasse bzgl der Äquivalenzrelation parallelgleich,
d.h, mit der Pfeilklasse 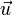 bezeichnet man die Menge aller zu dem Pfeil
bezeichnet man die Menge aller zu dem Pfeil 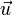 parallelgleicen Pfeile der Ebene bzw. des Raumes:
parallelgleicen Pfeile der Ebene bzw. des Raumes:
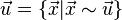
Rechenregeln der Addition von Pfeilklassen
Für beliebige Pfeilklassen 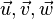 gilt:
gilt:
i) 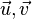 gilt
gilt 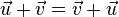 (Kommuntativität der Addition)
(Kommuntativität der Addition)
ii) 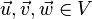 gilt
gilt 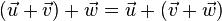 (Assoziativität der Addition)
(Assoziativität der Addition)
iii) Es existiert eine Pfeilklasse 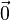 , sodass gilt
, sodass gilt 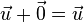 (neutrales Element bzgl. der Addition, Nullpfeilklasse)
(neutrales Element bzgl. der Addition, Nullpfeilklasse)
iv) Zu jedem 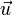 existiert ein
existiert ein 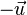 mit
mit 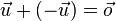 (inverses Element)
(inverses Element)

