Lösung von Aufgabe 4.08 S SoSe 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Lösung User ...) |
*m.g.* (Diskussion | Beiträge) (→Bemerkung --*m.g.* 23:20, 3. Jun. 2013 (CEST)) |
||
| Zeile 21: | Zeile 21: | ||
# Formulieren Sie bei Widerspruchsbeweisen explizit die Annahme: <math>a \not || b</math> | # Formulieren Sie bei Widerspruchsbeweisen explizit die Annahme: <math>a \not || b</math> | ||
| + | # Außen- bzw. Innenwinkel wovon? Machen Sie eine Skizze, auf die Sie sich beziehen (Auf Papier mit dem Smartphone photographieren und hier hochladen. | ||
==Lösung User ...== | ==Lösung User ...== | ||
Aktuelle Version vom 3. Juni 2013, 22:22 Uhr
Aufgabe 4.08Gegeben seien in der Ebene Lösung User ...Vor.:
Bemerkung --*m.g.* 23:20, 3. Jun. 2013 (CEST)Ich erkenne die richtige Beweisidee. Die Formulierung Ihres Beweises bedarf der Überarbeitung:
Lösung User ...Lösung User ...
|
 zwei nicht identische Geraden
zwei nicht identische Geraden  und
und  . Sowohl
. Sowohl  jeweils in genau einem Punkt geschnitten werden. Beweisen Sie: Wenn bei diesem Schnitt kongruente Stufenwinkel entstehen, dann sind
jeweils in genau einem Punkt geschnitten werden. Beweisen Sie: Wenn bei diesem Schnitt kongruente Stufenwinkel entstehen, dann sind 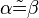
 ein Innenwinkel und
ein Innenwinkel und  ein Außenwinkel ist.
ein Außenwinkel ist.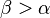 wegen dem schwachen Außenwinkelsatz.
Dies ist ein Widerspruch zur Voraussetzung.
wegen dem schwachen Außenwinkelsatz.
Dies ist ein Widerspruch zur Voraussetzung.