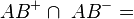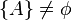Lösung von Aufgabe 6.04 S SoSe 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) |
Illu13 (Diskussion | Beiträge) (→Lösung User ...) |
||
| Zeile 14: | Zeile 14: | ||
| − | ==Lösung User .. | + | ==Lösung User --[[Benutzer:Illu13|Illu13]] 20:22, 6. Jun. 2013 (CEST)== |
| + | |||
| + | Die Zerlegung der Gerade AB in die Halbgeraden <math>\ AB^{+} und \ AB^{-}</math> ist keine Klasseneinteilung von AB, weil die dritte Voraussetzung für eine Klasseneinteilung nicht erfüllt ist. | ||
| + | |||
| + | Die dritte Voraussetzung besagt nämlich, dass die Teilmengen keine Elemente gemeinsam haben, d.h. der paarweise Schnitt der einzelnen Teilmengen ist die leere Menge. Die Halbgeraden <math>\ AB^{+} und \ AB^{-}</math> enthalten aber beide den Punkt A. Somit wäre das ein Widerspruch zur dritten Voraussetzung. | ||
| + | |||
| + | <math>\ AB^{+} \cap \ AB^{-} =</math> <math>\{A\} \neq \phi</math> | ||
| + | |||
| + | --[[Benutzer:Illu13|Illu13]] 20:22, 6. Jun. 2013 (CEST) | ||
==Lösung User ...== | ==Lösung User ...== | ||
Aktuelle Version vom 6. Juni 2013, 19:22 Uhr
Aufgabe 6.04Es seien Begründen Sie, warum die Zerlegung einer Geraden
Lösung User --Illu13 20:22, 6. Jun. 2013 (CEST)Die Zerlegung der Gerade AB in die Halbgeraden Die dritte Voraussetzung besagt nämlich, dass die Teilmengen keine Elemente gemeinsam haben, d.h. der paarweise Schnitt der einzelnen Teilmengen ist die leere Menge. Die Halbgeraden
--Illu13 20:22, 6. Jun. 2013 (CEST) Lösung User ...Lösung User ...
|
 eine Menge und
eine Menge und 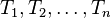 Teilmengen von
Teilmengen von 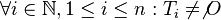
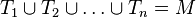
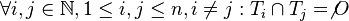
 in die Halbgeraden
in die Halbgeraden  und
und  keine Klasseneinteilung von
keine Klasseneinteilung von 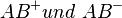 ist keine Klasseneinteilung von AB, weil die dritte Voraussetzung für eine Klasseneinteilung nicht erfüllt ist.
ist keine Klasseneinteilung von AB, weil die dritte Voraussetzung für eine Klasseneinteilung nicht erfüllt ist.