Lösung von Aufgabe 6.07 S SoSe 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
Illu13 (Diskussion | Beiträge) (→Lösung User ...) |
||
| Zeile 8: | Zeile 8: | ||
Wenn <math> C \in \ AB^{+} </math> und <math>\left| AB \right| < \left| AC \right| </math> dann gilt <math>\operatorname Zw (A, B, C) </math> <br /><br /> | Wenn <math> C \in \ AB^{+} </math> und <math>\left| AB \right| < \left| AC \right| </math> dann gilt <math>\operatorname Zw (A, B, C) </math> <br /><br /> | ||
| − | ==Lösung User ...== | + | ==Lösung User --[[Benutzer:Illu13|Illu13]] 21:07, 6. Jun. 2013 (CEST)== |
| + | |||
| + | <u>z.z.</u>: <math>C\in \ AB^{+} \wedge \left| AB \right| < \left| AC \right| \Rightarrow Zw(A,B,C)</math> | ||
| + | |||
| + | 1.Voraussetzung: <math>C\in \ AB^{+}</math> | ||
| + | |||
| + | 2.Voraussetzung: <math>\left| AB \right| < \left| AC \right|</math> (*) | ||
| + | |||
| + | Behauptung: Zw(A,B,C) | ||
| + | |||
| + | <u>Beweis:</u> | ||
| + | |||
| + | <math>C\in \ AB^{+}</math> <math>\Rightarrow</math> Zw(A,B,C) <math> \vee</math> Zw(A,C,B) [s. Def. Halbgerade] | ||
| + | |||
| + | nun z.z.: <math>\neg Zw(A,C,B)</math> | ||
| + | |||
| + | Annahme: Zw(A,C,B) <math>\Leftrightarrow</math> <math>\left| AC \right| + \left| CB \right| = \left| AB \right| \Leftrightarrow \left| AC \right| + \left| BC \right| = \left| AB \right|</math> (**) (s. Axiom II.2) | ||
| + | |||
| + | aus (*) und (**) folgt: | ||
| + | |||
| + | <math>\left| AB \right| < \left| AC \right| \Leftrightarrow \left| AC \right| + \left| BC \right| <\left| AC \right| \Leftrightarrow \left| BC \right| < 0 \Rightarrow</math> Widerspruch zu Axiom II.1 (Der Abstand zwei beliebiger Punkte ist nie negativ.) | ||
| + | |||
| + | Daher gilt: Zw(A,B,C) q.e.d. | ||
| + | |||
| + | --[[Benutzer:Illu13|Illu13]] 21:07, 6. Jun. 2013 (CEST) | ||
==Lösung User ...== | ==Lösung User ...== | ||
Aktuelle Version vom 6. Juni 2013, 21:07 Uhr
Aufgabe 6.07Zeigen Sie, dass für drei paarweise verschiedene Punkte Lösung User --Illu13 21:07, 6. Jun. 2013 (CEST)z.z.: 1.Voraussetzung: 2.Voraussetzung: Behauptung: Zw(A,B,C) Beweis:
nun z.z.: Annahme: Zw(A,C,B) aus (*) und (**) folgt:
Daher gilt: Zw(A,B,C) q.e.d. --Illu13 21:07, 6. Jun. 2013 (CEST) Lösung User ...Lösung User ...
|
 und
und  gilt:
gilt: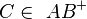 und
und 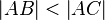 dann gilt
dann gilt 
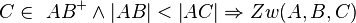
 Zw(A,B,C)
Zw(A,B,C) 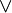 Zw(A,C,B) [s. Def. Halbgerade]
Zw(A,C,B) [s. Def. Halbgerade]
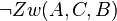

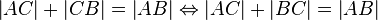 (**) (s. Axiom II.2)
(**) (s. Axiom II.2)
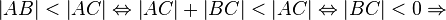 Widerspruch zu Axiom II.1 (Der Abstand zwei beliebiger Punkte ist nie negativ.)
Widerspruch zu Axiom II.1 (Der Abstand zwei beliebiger Punkte ist nie negativ.)

